
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
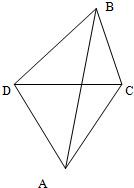 如图,我炮兵阵地位于A处,两观察所分别设于C,D,已知△ACD为边长等于a的正三角形.当目标出现于B时,测得∠CDB=45°,∠BCD=75°,试求炮击目标的距离AB.(结果保留根式形式)
如图,我炮兵阵地位于A处,两观察所分别设于C,D,已知△ACD为边长等于a的正三角形.当目标出现于B时,测得∠CDB=45°,∠BCD=75°,试求炮击目标的距离AB.(结果保留根式形式)查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,我炮兵阵地位于A处,两观察所分别设于C、D,已知△ACD为边长等于a的正三角形.若目标出现于B时,测得∠CDB=45°,∠BCD=75°,则炮击目标AB的距离为
如图,我炮兵阵地位于A处,两观察所分别设于C、D,已知△ACD为边长等于a的正三角形.若目标出现于B时,测得∠CDB=45°,∠BCD=75°,则炮击目标AB的距离为
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
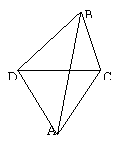 如图,我炮兵阵地位于A处,两观察所分别设于C,D,已知△ACD为边长等于
如图,我炮兵阵地位于A处,两观察所分别设于C,D,已知△ACD为边长等于![]() 的正三角形.当目标出现于B时,测得∠CDB=45°,∠BCD=75°,试求炮击目标的距离AB.(结果保留根式形式)
的正三角形.当目标出现于B时,测得∠CDB=45°,∠BCD=75°,试求炮击目标的距离AB.(结果保留根式形式)
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省开封市尉氏县民开高级中学高二(上)月考数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com