
【题目】如图,正三棱柱ABCA1B1C1中,AB=2,AA1=3,
D为C1B的中点,P为AB边上的动点.
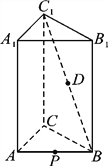
(1)当点P为AB的中点时,证明DP∥平面ACC1A1;
(2)若AP=3PB,求三棱锥BCDP的体积.
【答案】(1)见解析;(2)![]()
【解析】试题分析:(1)连结DP,AC1,推导出DP∥AC1,由此能证明DP∥平面ACClAl. (2)过点D作DE⊥BC于E,则DE平行且等于![]() CC1,∵CC1⊥平面ABC,∴DE⊥平面BCP,根据等体积转化VB-CDP=VD-BCP=
CC1,∵CC1⊥平面ABC,∴DE⊥平面BCP,根据等体积转化VB-CDP=VD-BCP=![]() ·S△BCP·DE.即得解
·S△BCP·DE.即得解
试题解析:
(1)连结DP,AC1,∵P为AB中点,D为C1B中点,∴DP∥AC1.又∵AC1平面ACC1A1,DP平面ACC1A1,∴DP∥平面ACC1A1。
(2)由AP=3PB,得PB=![]() AB=
AB=![]() .过点D作DE⊥BC于E,
.过点D作DE⊥BC于E,
则DE平行且等于![]() CC1,∵CC1⊥平面ABC,∴DE⊥平面BCP,
CC1,∵CC1⊥平面ABC,∴DE⊥平面BCP,
又∵CC1=3,∴DE=![]() .
.
∴VB-CDP=VD-BCP=![]() ·S△BCP·DE=
·S△BCP·DE=![]() ×
×![]() ×2×
×2×![]() ×sin60°×
×sin60°×![]() =
=![]()


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知A(-![]() ,0),B(0,-
,0),B(0,-![]() ),其中k≠0且k≠±1,直线l经过点P(1,0)和AB的中点.
),其中k≠0且k≠±1,直线l经过点P(1,0)和AB的中点.
(1)求证:A,B关于直线l对称.
(2)当1<k<![]() 时,求直线l在y轴上的截距b的取值范围.
时,求直线l在y轴上的截距b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据第2题求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x3+bx2+cx+d的图象如图,则函数 ![]() 的单调递减区间是( )
的单调递减区间是( ) 
A.(﹣∞,﹣2)
B.(﹣∞,1)
C.(﹣2,4)
D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学对高三学生进行体能测试,已知高三某文科班有学生30人,立定跳远的测试成绩用茎叶图表示如图(单位: ![]() );男生成绩在
);男生成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格”;女生成绩在
)定义为“不合格”;女生成绩在![]() 以上(包括
以上(包括![]() )定义为“合格”,成绩在
)定义为“合格”,成绩在![]() 以下(不包括
以下(不包括![]() )定义为“不合格.
)定义为“不合格.

(1)求女生立定跳远测试成绩的中位数;
(2)若在男生中按成绩是否合格进行分层抽样,抽取6人,求抽取成绩为“合格”的学生人数;
(3)若从(2)中抽取的6名男生中任意选取4人,求这4人中至少有3人“合格”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果对定义在R上的函数f(x)对任意两个不相等的实数x1 , x2 , 都有(x1﹣x2)[f(x1)﹣f(x2)]>0,则称函数f(x)为“H函数”.给出下列函数①y=﹣x3+x+1;②y=3x﹣2(sinx﹣cosx);③y=ex+1;④ ![]() .其中“H函数”的个数为( )
.其中“H函数”的个数为( )
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在![]() 上的函数
上的函数![]() ,如果满足:对任意
,如果满足:对任意![]() ,存在常数
,存在常数![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 是
是![]() 上的有界函数,其中
上的有界函数,其中![]() 称为函数
称为函数![]() 的上界.
的上界.
(![]() )判断函数
)判断函数![]() ,
, ![]() 是否是有界函数,请写出详细判断过程.
是否是有界函数,请写出详细判断过程.
(![]() )试证明:设
)试证明:设![]() ,
, ![]() ,若
,若![]() ,
, ![]() 在
在![]() 上分别以
上分别以![]() ,
, ![]() 为上界,求证:函数
为上界,求证:函数![]() 在
在![]() 上以
上以![]() 为上界.
为上界.
(![]() )若函数
)若函数![]() 在
在![]() 上是以
上是以![]() 为上界的有界函数,求实数
为上界的有界函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn}满足a1=2,b1=4,且 2bn=an+an+1 , an+12=bnbn+1 .
(Ⅰ)求 a 2 , a3 , a4及b2 , b3 , b4;
(Ⅱ)猜想{an},{bn}的通项公式,并证明你的结论;
(Ⅲ)证明:对所有的 n∈N* , ![]()
![]() …
… ![]() <
< ![]() <
< ![]() sin
sin ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com