
科目:高中数学 来源:2017届重庆市高三上学期期中数学(理)试卷(解析版) 题型:解答题
根据某电子商务平台的调查统计显示,参与调查的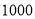 位上网购物者的年龄情况如下图.
位上网购物者的年龄情况如下图.
(1)已知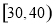 、
、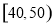 、
、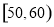 三个年龄段的上网购物者人数成等差数列,求
三个年龄段的上网购物者人数成等差数列,求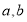 的值;
的值;
(2)该电子商务平台将年龄在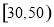 之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放
之间的人群定义为高消费人群,其他的年龄段定义为潜在消费人群,为了鼓励潜在消费人群的消费,该平台决定发放代金券,高消费人群每人发放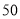 元的代金券,潜在消费人群每人发放
元的代金券,潜在消费人群每人发放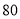 元的代金券.已经采用分层抽样的方式从参与调查的
元的代金券.已经采用分层抽样的方式从参与调查的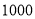 位上网购物者中抽取了
位上网购物者中抽取了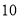 人,现在要在这
人,现在要在这 人中随机抽取
人中随机抽取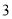 人进行回访,求此三人获得代金券总和
人进行回访,求此三人获得代金券总和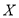 的分布列与数学期望.
的分布列与数学期望.

查看答案和解析>>
科目:高中数学 来源:2017届山东德州市高三上学期期中数学(文)试卷(解析版) 题型:填空题
定义: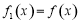 ,当
,当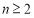 且
且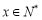 时,
时,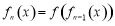 ,对于函数
,对于函数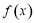 定义域内的
定义域内的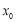 ,若正在正整数
,若正在正整数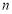 是使得
是使得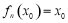 成立的最小正整数,则称
成立的最小正整数,则称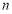 是点
是点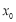 的最小正周期,
的最小正周期,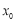 称为
称为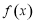 的
的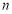 ~周期点,已知定义在
~周期点,已知定义在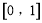 上的函数
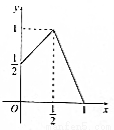
上的函数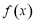 的图象如图,对于函数
的图象如图,对于函数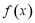 ,下列说法正确的是 (写出所有正确命题的编号.
,下列说法正确的是 (写出所有正确命题的编号.
①1是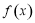 的一个3~周期点;
的一个3~周期点;
②3是点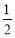 的最小正周期;
的最小正周期;
③对于任意正整数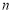 ,都有
,都有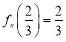 ;
;
④若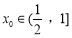 ,则
,则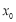 是
是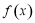 的一个2~周期点.
的一个2~周期点.
查看答案和解析>>
科目:高中数学 来源:2017届贵州遵义市高三上学期期中数学(文)试卷(解析版) 题型:解答题
已知函数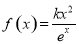 ,其中
,其中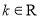 且
且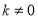 .
.
(1)求函数 的单调区间;
的单调区间;
(2)当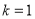 时,若存在
时,若存在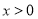 ,使
,使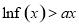 成立,求实数
成立,求实数 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com