
【题目】已知函数![]() 在点
在点![]() 处的切线与y轴垂直.
处的切线与y轴垂直.
(1)若![]() ,求
,求![]() 的单调区间;
的单调区间;
(2)若![]() ,
,![]() 成立,求a的取值范围
成立,求a的取值范围
【答案】(1)见解析;(2)
【解析】
(1)令f′(1)=0求出b,再根据f′(x)的符号得出f(x)的单调区间;
(2)分类讨论,分别求出![]() 在(0,e)上的最小值,即可得出a的范围.
在(0,e)上的最小值,即可得出a的范围.
(1)![]() ,由题
,由题![]() ,
,
解得![]() ,由
,由![]() ,得
,得![]() .
.
因为![]() 的定义域为
的定义域为![]() ,所以
,所以![]() ,
,
故当![]() 时,
时,![]() ,
, ![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
(2)由(1)知![]() ,
,
所以![]()
(ⅰ)若![]() ,则由(1)知
,则由(1)知![]() ,即
,即![]() 恒成立
恒成立
(ⅱ)若![]() ,则
,则 且
且![]()
故当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
![]() ,即
,即![]() 恒成立
恒成立
(ⅲ)若![]() ,则
,则 且
且![]()
故当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
由题只需![]() 即可,即
即可,即![]() ,解得
,解得![]() ,
,
而由![]() ,且
,且![]() ,
,
得![]()
(ⅳ)若![]() ,则
,则![]() ,
,![]() 为增函数,且
为增函数,且![]() ,
,
所以![]() ,
,![]() ,不合题意,舍去;
,不合题意,舍去;
(ⅴ)若![]() ,则
,则![]() ,
,![]() 在
在![]() 上都为增函数,且
上都为增函数,且![]()
所以![]() ,
,![]() ,不合题意,舍去;
,不合题意,舍去;
综上所述,a的取值范围是


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】湖北省第二届(荆州)园林博览会于2019年9月28日至11月28日在荆州园博园举办,本届园林博览会以“辉煌荆楚,生态园博”为主题,展示荆州生态之美,文化之韵,吸引更多优秀企业来荆投资,从而促进荆州经济快速发展.在此博览会期间,某公司带来了一种智能设备供采购商洽谈采购,并决定大量投放荆州市场.已知该种设备年固定研发成本为50万元,每生产一台需另投入80元,设该公司一年内生产该设备![]() 万台,且全部售完,且每万台的销售收入
万台,且全部售完,且每万台的销售收入![]() (万元)与年产量
(万元)与年产量![]() (万台)的函数关系式近似满足
(万台)的函数关系式近似满足
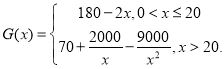
(1)写出年利润![]() (万元)关于年产量
(万元)关于年产量![]() (万台)的函数解析式.(年利润
(万台)的函数解析式.(年利润![]() 年销售收入
年销售收入![]() 总成本).
总成本).
(2)当年产量为多少万台时,该公司获得的利润最大?并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于两个定义域相同的函数![]() 、
、![]() ,若存在实数
,若存在实数![]() 、
、![]() 使
使![]() ,则称函数
,则称函数![]() 是由“基函数
是由“基函数![]() 、
、![]() ”生成的.
”生成的.
(1)![]() 和
和![]() 生成一个偶函数
生成一个偶函数![]() ,求
,求![]() 的值;
的值;
(2)若![]() 由
由![]() ,
,![]() (
(![]() 且
且![]() )生成,求
)生成,求![]() 的取值范围;
的取值范围;
(3)试利用“基函数![]() ,
,![]() ”生成一个函数
”生成一个函数![]() ,使
,使![]() 满足下列条件:①是偶函数;②有最小值1,请求出函数
满足下列条件:①是偶函数;②有最小值1,请求出函数![]() 的解析式并进一步研究该函数的单调性(无需证明).
的解析式并进一步研究该函数的单调性(无需证明).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,将三角形
的中点,将三角形![]() 沿
沿![]() 折起,则下列说法正确的是______________.
折起,则下列说法正确的是______________.
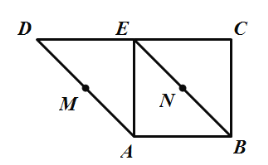
(1)不论![]() 折至何位置(不在平面
折至何位置(不在平面![]() 内),都有
内),都有![]() 平面
平面![]() ;
;
(2)不论![]() 折至何位置,都有
折至何位置,都有![]() ;
;
(3)不论![]() 折至何位置(不在平面
折至何位置(不在平面![]() 内),都有
内),都有![]() ;
;
(4)在折起过程中,一定存在某个位置,使![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一项自“一带一路”沿线20国青年参与的评选中“高铁”、“支付宝”、“共享单车”和“网购”被称作中国“新四大发明”,曾以古代“四大发明”推动世界进步的中国,正再次以科技创新向世界展示自己的发展理念.某班假期分为四个社会实践活动小组,分别对“新四大发明”对人们生活的影响进行调查.于开学进行交流报告会.四个小组随机排序,则“支付宝”小组和“网购”小组不相邻的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,且
,且![]() 为正三角形,
为正三角形,![]() ,
,![]() 为
为![]() 的中点.
的中点.
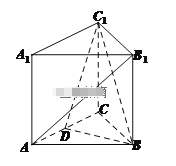
(1)求证:直线![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)三棱柱![]() 的顶点都在一个球面上,求该球的体积.
的顶点都在一个球面上,求该球的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com