练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    在等差数列{an}中，若a1003+a1004+a1005+a1006=18，则该数列的前2008项的和为


    1. A.
      18072
    2. B.
      3012
    3. C.
      9036
    4. D.
      12048
    C
    分析：利用等差数列的性质化简已知的等式，求出a1+a2008的值，然后利用等差数列的前n项和公式表示出该数列的前2008项的和，将a1+a2008的值代入即可求出值．
    解答：∵a1003+a1004+a1005+a1006
    =（a1003+a1006）+（a1004+a1005）
    =2（a1+a2008）=18，
    ∴a1+a2008=9，
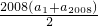
    则S2008==1004（a1+a2008）=1004×9=9036．
    故选C
    点评：此题考查了等差数列的性质，以及等差数列的前n项和公式，熟练掌握性质及公式是解本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1=-2010，其前n项的和为Sn．若
    S2010
    2010
    -
    S2008
    2008
    =2，则S2010=（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，a1+3a8+a15=60，则2a9-a10的值为
    12
    12
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知在等差数列{an}中，d＞0，a2008、a2009是方程x2-3x-5=0的两个根，那么使得前n项和Sn为负值的最大的n的值是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，已知a1=2，a2+a3=13，则a4+a5+a6等于=
    42
    42
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    在等差数列{an}中，若S4=1，S8=4，则a17+a18+a19+a20的值=
    9
    9
    ．

    查看答案和解析>>

    同步练习册答案