练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】某校进入高中数学竞赛复赛的学生中，高一年级有8人，高二年级有16人，高三年级有32人，现釆用分层抽样的方法从这些学生中抽取7人进行釆访.

    （1）求应从各年级分别抽取的人数；

    （2）若从抽取的7人中再随机抽取2人做进一步了解（注高一学生记为，高二学生记为，高三学生记为，

    ①列出所有可能的抽取结果；

    ②求抽取的2人均为高三年级学生的概率.

    【答案】（1）高一1人，高二2人，高三4人（2）①具体抽取结果见解析；②.

    【解析】

    （1）根据分层抽样等比例抽取的性质，即可列式计算；

    （2）①根据题意，列举即可；

    ②计算出所有基本事件的个数，再找出满足题意的事件个数，用古典概型的概率计算公式即可求得.

    （1）高一：；

    高二：；

    高三：

    所以抽取高一1人，高二2人，高三4人.

    （2）由（1）知高一1人记为，高二2人记为，高三4人记为，

    ①从中抽取两人，所有可能的结果为：

    ，

    共21种.

    ②由①知，共有21种情况，抽取的2人均为高三年级学生有

    ，共6种，

    所以抽取的2人均为高三年级学生的概率.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知两个不相等的非零向量，，两组向量，，，，和，，，，，均由2个和3个排列而成，记，表示S所有可能取值中的最小值，则下列命题正确的是________．（写出所有正确命题的编号）

    ①S有5个不同的值；②若，则与无关；③若，则与无关；④若，则；⑤若，，则与的夹角为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在正方体ABCD-A1B1C1D1中，E，F分别是C1D1，CC1的中点，则异面直线AE与BF所成角的余弦值为（　　）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知某校一间办公室有四位老师甲、乙、丙、丁．在某天的某个时段，他们每人各做一项工作，一人在查资料，一人在写教案，一人在批改作业，另一人在打印材料．

    若下面4个说法都是正确的：

    ①甲不在查资料，也不在写教案； ②乙不在打印材料，也不在查资料；

    ③丙不在批改作业，也不在打印材料； ④丁不在写教案，也不在查资料．

    此外还可确定：如果甲不在打印材料，那么丙不在查资料．根据以上信息可以判断

    A．甲在打印材料

    B．乙在批改作业

    C．丙在写教案

    D．丁在打印材料

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】据历史记载，美日在中途岛(Midway)海战前，美方截获了日方密码电报，据美方已破译的密码得知，日方将向某岛进行军事活动，但关键含有地点的部分却被日方换成了另一种密码．经专家研究，估计是一种密匙密码，且密匙为3位．所谓密匙密码是指：将一段英文字母的明文(未加密前原文)经过对某一组数字(即密匙)的变换，改变成了另一组英文字母成为密文(加密后的文字)例如：明文： (不计空格，不计大小写)在密匙为：1 9 2的条件下，变换过程如下图所示：

    s

    t

    u

    d

    e

    n

    t

    1

    9

    2

    1

    9

    2

    1

    t

    c

    w

    e

    n

    p

    u

    则密文为：，试根据上面信息回答下面问题：

    （1）在密匙为111的条件下，填写下表，并写出密文；

    s

    t

    u

    d

    e

    n

    t

    密文____________________．

    （2）若请填写下表，并写出密匙；

    s

    t

    u

    d

    e

    n

    t

    密匙为_____________．

    （3)若下面即是那段包含地点(Midway)的破译不出的密文：,且此段密文也是3位密匙加密，试填写下表，写出密匙，并将此段密文翻译成明文．（不必证明，写出明文即可）

    c

    w

    b

    c

    f

    s

    o

    l

    l

    y

    d

    g

    密匙为___________，明文为_________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，等腰中，，，点，，为线段的四等分点，且.现沿，，折叠成图2所示的几何体，使.

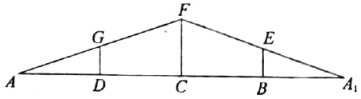
    （图1）

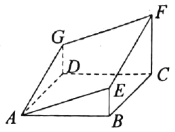
    （图2）

    （1）证明：平面；

    （2）求几何体的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在三棱锥中，，，，，.

    (Ⅰ)求证：平面平面；

    (Ⅱ)为棱上一点，试确定点的位置，使得直线与平面所成角的正弦值为.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2017年1月至2019年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（　　）

    A.年接待游客量逐年增加

    B.各年的月接待游客量高峰期大致在8月

    C.2017年1月至12月月接待游客量的中位数为30万人

    D.各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对于无穷数列，若对任意，满足且（是与无关的常数），则称数列为数列.

    （1）若（），判断数列是否为数列，说明理由；

    （2）设，求证：数列是数列，并求常数的取值范围；

    （3）设数列（，），问数列是否为数列？说明理由.

    查看答案和解析>>

    同步练习册答案