
①对任意两个事件A、B都有P(A·B)=P(A)·P(B);
②如果事件A发生,事件B一定发生,则P(A·B)=P(B);
③已知在一次试验中P(A)=0.1,那么在3次独立重复试验中A恰好发生2次的概率是![]() ·(0.1) 3-2·(0.9)2=3×0.1×0.81=0.243;
·(0.1) 3-2·(0.9)2=3×0.1×0.81=0.243;
④抛掷一枚硬币100次,则正面向上出现的次数超过40次.
请把正确命题的序号填在横线上:_______________.
科目:高中数学 来源: 题型:
| b |
| 3a |
| b |
| 3a |
| 1 |
| 3 |
| 1 |
| 2 |
| 5 |
| 12 |
| 1 |
| 2012 |
| 2 |
| 2012 |
| 3 |
| 2012 |
| 2011 |
| 2012 |
查看答案和解析>>
科目:高中数学 来源:2014届安徽省高二下学期期末质检理科数学试卷(解析版) 题型:填空题
对于三次函数 ,定义
,定义 是
是 的导函数
的导函数 的导函数,若方程
的导函数,若方程 有实数解
有实数解 ,则称点
,则称点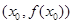 为函数
为函数 的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
的“拐点”,可以证明,任何三次函数都有“拐点”,任何三次函数都有对称中心,且“拐点”就是对称中心,请你根据这一结论判断下列命题:
①任意三次函数都关于点 对称:
对称:
②存在三次函数 有实数解
有实数解 ,点
,点 为函数
为函数 的对称中心;
的对称中心;
③存在三次函数有两个及两个以上的对称中心;
④若函数 ,则,
,则,
其中正确命题的序号为 (把所有正确命题的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com