
【题目】已知![]() 为椭圆
为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆
在椭圆![]() 上移动时,
上移动时, ![]() 的内心
的内心![]() 的轨迹方程为__________.
的轨迹方程为__________.
【答案】![]()
【解析】考查更为一般的问题:设P为椭圆C: ![]() 上的动点,
上的动点, ![]() 为椭圆的两个焦点,
为椭圆的两个焦点, ![]() 为△PF1F2的内心,求点I的轨迹方程.
为△PF1F2的内心,求点I的轨迹方程.
解法一:如图,设内切圆I与F1F2的切点为H,半径为r,且F1H=y,F2H=z,PF1=x+y,PF2=x+z, ![]() ,则
,则![]() .
.

直线IF1与IF2的斜率之积: ![]() ,
,
而根据海伦公式,有△PF1F2的面积为![]()
因此有![]() .
.
再根据椭圆的斜率积定义,可得I点的轨迹是以F1F2为长轴,
离心率e满足![]() 的椭圆,
的椭圆,
其标准方程为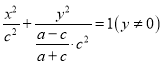 .
.
解法二:令![]() ,则
,则![]() .三角形PF1F2的面积:
.三角形PF1F2的面积:
![]() ,
,
其中r为内切圆的半径,解得![]() .
.
另一方面,由内切圆的性质及焦半径公式得:
![]()
从而有![]() .消去θ得到点I的轨迹方程为:
.消去θ得到点I的轨迹方程为:
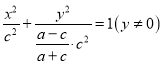 .
.
本题中: ![]() ,代入上式可得轨迹方程为:
,代入上式可得轨迹方程为: ![]() .
.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】在框图中,设x=2,并在输入框中输入n=4;ai=i(i=0,1,2,3,4).则此程序执行后输出的S值为( ) 
A.26
B.49
C.52
D.98
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,四边形
,四边形![]() 为矩形,
为矩形, ![]() ,平面
,平面![]() 平面
平面![]() .
.
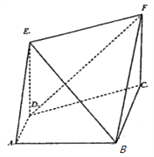
(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值;
所成锐二面角的余弦值;
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,若存在,求出线段
,若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知{an}为等差数列,前n项和为Sn(n∈N*),{bn}是首项为2的等比数列,且公比大于0,b2+b3=12,b3=a4-2a1,S11=11b4.
(Ⅰ)求{an}和{bn}的通项公式;
(Ⅱ)求数列{a2nbn}的前n项和(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCP中,CP∥AB,CP⊥CB,![]() ,CP=2,D是CP的中点,将△PAD沿AD折起,使得PD⊥面ABCD.
,CP=2,D是CP的中点,将△PAD沿AD折起,使得PD⊥面ABCD.

(1)求证:平面PAD⊥平面PCD;
(2)若E是PC的中点,求三棱锥D﹣PEB的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解篮球爱好者小李的投篮命中率与打篮球时间之间的关系,下表记录了小李某月1号到5号每天打篮球时间x(单位:小时)与当天投篮命中率y之间的关系:
时间x | 1 | 2 | 3 | 4 | 5 |
命中率y | 0.4 | 0.5 | 0.6 | 0.6 | 0.4 |
小李这5天的平均投篮命中率为 ;用线性回归分析的方法,预测小李该月6号打6小时篮球的投篮命中率为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,左右焦点分别为
,左右焦点分别为![]() 和
和![]() ,以点
,以点![]() 为圆心,以
为圆心,以![]() 为半径的圆与以点
为半径的圆与以点![]() 为圆心,以
为圆心,以![]() 为半径的圆相交,且交点在椭圆
为半径的圆相交,且交点在椭圆![]() 上.
上.
(![]() )求椭圆
)求椭圆![]() 的方程.
的方程.
(![]() )设椭圆
)设椭圆![]() ,
,![]() 为椭圆
为椭圆![]() 上任意一点,过点
上任意一点,过点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 、
、![]() 两点,射线
两点,射线![]() 交椭圆
交椭圆![]() 于点
于点![]() .
.
①求![]() 的值.
的值.
②求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一盒中装有9张各写有一个数字的卡片,其中4张卡片上的数字是1,3张卡片上的数字是2,2张卡片上的数字是3,从盒中任取3张卡片.
(1)求所取3张卡片上的数字完全相同的概率;
(2)X表示所取3张卡片上的数字的中位数,求X的分布列与数学期望.(注:若三个数字a,b,c满足a≤b≤c,则称b为这三个数的中位数.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com