
【题目】已知![]() ,数列
,数列![]() 、
、![]() 满足:
满足:![]() ,
,![]() ,记
,记![]() .
.
(1)若![]() ,
,![]() ,求数列
,求数列![]() 、
、![]() 的通项公式;
的通项公式;
(2)证明:数列![]() 是等差数列;
是等差数列;
(3)定义![]() ,证明:若存在
,证明:若存在![]() ,使得
,使得![]() 、
、![]() 为整数,且
为整数,且![]() 有两个整数零点,则必有无穷多个
有两个整数零点,则必有无穷多个![]() 有两个整数零点.
有两个整数零点.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】若数列![]() 中存在三项,按一定次序排列构成等比数列,则称
中存在三项,按一定次序排列构成等比数列,则称![]() 为“等比源数列”。
为“等比源数列”。
(1)在无穷数列![]() 中,
中,![]() ,
,![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)在(1)的结论下,试判断数列![]() 是否为“等比源数列”,并证明你的结论;
是否为“等比源数列”,并证明你的结论;
(3)已知无穷数列![]() 为等差数列,且
为等差数列,且![]() ,
,![]() (
(![]() ),求证:数列
),求证:数列![]() 为“等比源数列”.
为“等比源数列”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地区某种昆虫产卵数和温度有关.现收集了一只该品种昆虫的产卵数![]() (个)和温度
(个)和温度![]() (
(![]() )的7组观测数据,其散点图如所示:
)的7组观测数据,其散点图如所示:
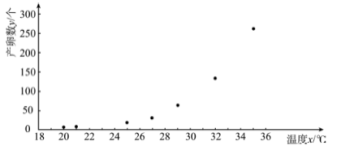
根据散点图,结合函数知识,可以发现产卵数![]() 和温度
和温度![]() 可用方程
可用方程![]() 来拟合,令
来拟合,令![]() ,结合样本数据可知
,结合样本数据可知![]() 与温度
与温度![]() 可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
可用线性回归方程来拟合.根据收集到的数据,计算得到如下值:
|
|
|
|
|
|
27 | 74 |
| 182 |
|
|
表中![]() ,
,![]() .
.
(1)求![]() 和温度
和温度![]() 的回归方程(回归系数结果精确到
的回归方程(回归系数结果精确到![]() );
);
(2)求产卵数![]() 关于温度
关于温度![]() 的回归方程;若该地区一段时间内的气温在
的回归方程;若该地区一段时间内的气温在![]() 之间(包括
之间(包括![]() 与
与![]() ),估计该品种一只昆虫的产卵数的范围.(参考数据:
),估计该品种一只昆虫的产卵数的范围.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .)
.)
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某沿海城市的海边有两条相互垂直的直线型公路l1、l2,海岸边界MPN近似地看成一条曲线段.为开发旅游资源,需修建一条连接两条公路的直线型观光大道AB,且直线AB与曲线MPN有且仅有一个公共点P(即直线与曲线相切),如图所示.若曲线段MPN是函数![]() 图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
图象的一段,点M到l1、l2的距离分别为8千米和1千米,点N到l2的距离为10千米,以l1、l2分别为x、y轴建立如图所示的平面直角坐标系xOy,设点P的横坐标为p.
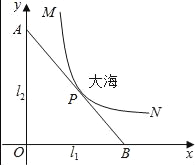
(1)求曲线段MPN的函数关系式,并指出其定义域;
(2)若某人从点O沿公路至点P观景,要使得沿折线OAP比沿折线OBP的路程更近,求p的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】自然状态下的鱼类是一种可再生资源,为了持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响.用![]() 表示某鱼群在第
表示某鱼群在第![]() 年年初的总量且
年年初的总量且![]() .不考虑其他因素,设在第
.不考虑其他因素,设在第![]() 年内鱼群的繁殖量及捕捞量都与
年内鱼群的繁殖量及捕捞量都与![]() 成正比,死亡量与
成正比,死亡量与![]() 成正比,这些比例系数依次为正常数
成正比,这些比例系数依次为正常数![]() ,
,![]() ,
,![]()
(1)求![]() 与
与![]() 的关系式
的关系式
(2)若每年年初鱼群的总量保持不变,求![]() ,
,![]() ,
,![]() ,
,![]() 所应满足的条件
所应满足的条件
(3)设![]() ,
,![]() ,为保证对任意
,为保证对任意![]() ,都有
,都有![]() ,则捕捞强度
,则捕捞强度![]() 的最大允许值是多少?并说明理由.
的最大允许值是多少?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若存在常数
,若存在常数![]() ,对任意
,对任意![]() 都有
都有![]() ,则称函数
,则称函数![]() 为T倍周期函数.
为T倍周期函数.
(1)判断![]() 是否是T倍周期函数,并说明理由;
是否是T倍周期函数,并说明理由;
(2)证明 是T倍周期函数,且T的值是唯一的;
是T倍周期函数,且T的值是唯一的;
(3)若![]() 是2倍周期函数,
是2倍周期函数,![]() ,
,![]() ,
,![]() 表示
表示![]() 的前n项和,
的前n项和,![]() ,若
,若![]() 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,对于点
中,对于点![]() ,定义变换
,定义变换![]() :将点
:将点![]() 变换为点
变换为点![]() ,使得
,使得![]() 其中
其中![]() .这样变换
.这样变换![]() 就将坐标系
就将坐标系![]() 内的曲线变换为坐标系
内的曲线变换为坐标系![]() 内的曲线.则四个函数
内的曲线.则四个函数![]() ,
,![]() ,
,![]() ,
,![]() 在坐标系
在坐标系![]() 内的图象,变换为坐标系
内的图象,变换为坐标系![]() 内的四条曲线(如图)依次是
内的四条曲线(如图)依次是

A. ②,③,①,④B. ③,②,④,①C. ②,③,④,①D. ③,②,①,④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com