【题目】已知关于x的一元二次函数
，分别从集合
和
中随机取一个数
和
得到数对
．
（1）若
， 
，求函数
在
内是偶函数的概率；
（2）若
， 
，求函数
有零点的概率；
（3）若
， 
，求函数
在区间
上是增函数的概率．
【答案】（1）
；（2）
；（3）
．
【解析】试题分析：
（1）列出数对数对
的所有情况，根据函数为偶函数得
，然后由古典概型概率公式求解即可．（2）列出数对数对
的所有情况，由条件得要使
有零点，则满足
，然后由古典概型概率公式求解即可．（3）要使
单调递增，则需满足
，即
，然后根据几何概型概率公式求解．
试题解析：
（1）由已知得
， 
，
则分别从集合
和
中随机取一个数
和
得到数对
的所有可能的情况有： 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，共有18对．
要使
是偶函数，则须有
，故满足条件的有序数对有
， 
， 
，共有3对．
由古典概型概率公式可得所求概率为
．
故函数
在
内是偶函数的概率为
．
（2）由已知得， 
， 
，所有的有序数列有
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
， 
，共有18对．
要使
有零点，则需满足
，可得满足条件的有序数对有
， 
，
， 
， 
， 
，共有6对．
由古典概型概率公式可得所求概率为
．
故函数
有零点的概率为
．
（3）要使
单调递增，则需满足
，即
，
由题意得所有的基本事件构成的平面区域为
．
要使
单调递增，则需满足
，即
．
设“函数
在区间
上是增函数”为事件A，
则事件A包含的基本事件构成的平面区域为
．
由几何概型概率公式可得
．
故函数
在区间
上是增函数的概率为
．
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】已知关于x的不等式|x﹣a|＜b的解集为{x|2＜x＜4}．
（Ⅰ）求实数a，b的值；
（Ⅱ）设实数x，y，z 满足 
+ 
+ 
=1，求x，y，z的最大值和最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知等差数列{an}满足a1+a2=10,a5=a3+4.
(1)求{an}的通项公式;
(2)记{an}的前n项和为Sn若Sk+1<2ak+a2,求正整数k的值
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】2014年5月12日，国家统计局公布了《2013年农民工监测调查报告》，报告显示：我国农
民工收入持续快速增长．某地区农民工人均月收入增长率如图1，并将人均月收入绘制成如
图2的不完整的条形统计图．
图1 图2
根据以上统计图来判断以下说法错误的是
A. 2013年农民工人均月收入的增长率是
B. 2011年农民工人均月收入是
元
C. 小明看了统计图后说：“农民工2012年的人均月收入比2011年的少了”
D. 2009年到2013年这五年中2013年农民工人均月收入最高
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知圆M的圆心M在y轴上，半径为1．直线l：y=2x+2被圆M所截得的弦长为 
，且圆心M在直线l的下方．
（1）求圆M的方程；
（2）设A（t，0），B（t+5，0）（﹣4≤t≤﹣1），若AC，BC是圆M的切线，求△ABC面积的最小值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】若点O在
内，且满足
，设
为
的面积， 
为
的面积，则
＝________.
【答案】
【解析】由
，可得： 
延长OA，OB，OC，使OD=2OA，OE=4OB，OF=3OC，
如图所示：
∵2
+3
+4
=
，
∴
，
即O是△DEF的重心，
故△DOE，△EOF，△DOF的面积相等，
不妨令它们的面积均为1，
则△AOB的面积为
，△BOC的面积为
，△AOC的面积为
，
故三角形△AOB，△BOC，△AOC的面积之比依次为： 
： 
： 
=3：2：4，
.
故答案为： 
．
点睛：本题考查的知识点是三角形面积公式，三角形重心的性质，平面向量在几何中的应用，注意重要结论：点O在
内，且满足
， 
则三角形△AOB，△BOC，△AOC的面积之比依次为： 
.
【题型】填空题
【结束】
16
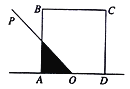
【题目】如图，正方形ABCD的边长为2，O为AD的中点，射线OP从OA出发，绕着点O顺时针方向旋转至OD，在旋转的过程中，记
为
OP所经过的在正方形ABCD内的区域（阴影部分）的面积
，那么对于函数
有以下三个结论：
①
；
②任意
，都有
；
③任意
且
，都有
.
其中正确结论的序号是__________. （把所有正确结论的序号都填上）.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在直角坐标系xOy中，过点P（2，1）的直线l的参数方程为 
（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρsin2θ=2cosθ，已知直线l与曲线C交于A、B两点．
（1）求曲线C的直角坐标方程；
（2）求|PA||PB|的值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】过椭圆 
=1的右焦点F作斜率k=﹣1的直线交椭圆于A，B两点，且 
共线．
（1）求椭圆的离心率；
（2）当三角形AOB的面积S△AOB= 
时，求椭圆的方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
