
【题目】椭圆![]() 的离心率为
的离心率为![]() ,且过点
,且过点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上任一点,
上任一点, ![]() 为其右焦点,点
为其右焦点,点![]() 满足
满足![]() .
.
①证明: ![]() 为定值;
为定值;
②设直线![]() 与椭圆
与椭圆![]() 有两个不同的交点
有两个不同的交点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() 成等差数列,求
成等差数列,求![]() 的值.
的值.
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
【题目】交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念,记交通指数为T,其范围为[0,10],分为五个级别,T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3),从某市交通指挥中心随机选取了三环以内的50个交通路段,依据其交通指数数据绘制的频率分布直方图如右图. (Ⅰ)这50个路段为中度拥堵的有多少个?
(Ⅱ)据此估计,早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少?
(III)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为36分钟;中度拥堵为42分钟;严重拥堵为60分钟,求此人所用时间的数学期望.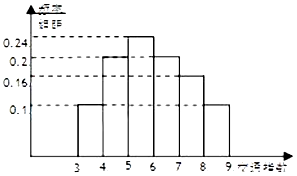
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=asinωx+bcosωx(0<ω<5,ab≠0)的图象的一条对称轴方程是 ![]() ,函数f'(x)的图象的一个对称中心是
,函数f'(x)的图象的一个对称中心是 ![]() ,则f(x)的最小正周期是( )
,则f(x)的最小正周期是( )
A.![]()
B.![]()
C.π
D.2π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xex﹣a(lnx+x).
(1)若函数f(x)恒有两个零点,求a的取值范围;
(2)若对任意x>0,恒有不等式f(x)≥1成立. ①求实数a的值;
②证明:x2ex>(x+2)lnx+2sinx.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.
组号 | 分组 | 频数 |
1 |
| 2 |
2 |
| 8 |
3 |
| 7 |
4 |
| 3 |
(Ⅰ)现从融合指数在![]() 和
和![]() 内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在
内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在![]() 的概率;
的概率;
(Ⅱ)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
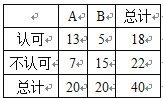
【题目】现在,很多人都喜欢骑“共享单车”,但也有很多市民并不认可.为了调查人们对这种交通方式的认可度,某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民,得到了一个市民是否认可的样本,具体数据如下![]() 列联表:
列联表:
附:![]() ,
,![]() .
.

根据表中的数据,下列说法中,正确的是( )
A. 没有95% 以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99% 以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年郴州市两会召开前夕,某网站推出两会热点大型调查,调查数据表明,民生问题时百姓最为关心的热点,参与调查者中关注此问题的约占80%,现从参与者中随机选出200人,并将这200人按年龄分组:第1组[15,25),第2组[25,35),第3组[35,45),第4组[45,55),第5组[55,65),得到的频率分布直方图如图所示. 
(1)求出频率分布直方图中的a值,并求出这200的平均年龄;
(2)现在要从年龄较小的第1,2,3组用分层抽样的方法抽取12人,再从这12人中随机抽取3人赠送礼品,求抽取的3人中至少有1人的年龄在第3组的概率;
(3)若要从所有参与调查的人(人数很多)中随机选出3人,记关注民生问题的人数为X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了100个蜜柚进行测重,其质量分别在![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (单位:克)中,其频率分布直方图如图所示.
(单位:克)中,其频率分布直方图如图所示.

(1)求质量落在![]() ,
, ![]() 两组内的蜜柚的抽取个数,
两组内的蜜柚的抽取个数,
(2)从质量落在![]() ,
, ![]() 内的蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
内的蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com