练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图是一个半径为3米的水轮，水轮圆心O距离水面2米，已知水轮每分钟转动四圈，水轮上的点P相对于水面的高度y（米）与时间x（秒）满足函数关系y=Asin（ωx+φ）+B（A＞0，ω＞0，0＜φ＜2π），若x=0时，P在最高点，则函数表达式为：    ．
    【答案】分析：先根据y的最大和最小值求得A和B，利用周期求得ω，当x=0时函数有最大值，进而求得φ的值，则函数的表达式可得．
    解答：解：依题意可知y的最大值为5，最小为-1
    ∴有求得B=2，A=3
    T==15
    ∴ω=
    x=0时，P在最高点，∴sinφ=1
    ∴φ=
    ∴函数的表达式为+2
    故答案为：+2
    点评：本题主要考查了在实际问题中建立三角函数模型的问题．考查了运用三角函数的最值，周期等问题确定函数的解析式．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

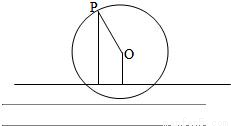
    精英家教网如图，一个半径为10米的水轮按逆时针方向每分钟转4圈，记水轮上的点P到水面的距离为d米（P在水面下则d为负数），则d（米）与时间t（秒）之间满足关系式：d=Asin（ωt+φ）+k（A＞0，ω＞0），-
    π
    2
    ＜φ＜
    π
    2
    ，且当P点从水面上浮现时开始计算时间，有以下四个结论：
    （1）A=10；
    （2）ω=
    2π
    15
    ；
    （3）φ=
    π
    6
    ；
    （4）K=5，
    则其中所有正确结论的序号是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

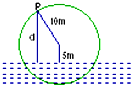
    精英家教网如图是一个半径为3米的水轮，水轮圆心O距离水面2米，已知水轮每分钟转动四圈，水轮上的点P相对于水面的高度y（米）与时间x（秒）满足函数关系y=Asin（ωx+φ）+B（A＞0，ω＞0，0＜φ＜2π），若x=0时，P在最高点，则函数表达式为：
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

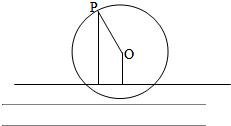
    如图是一个半径为3米的水轮，水轮圆心O距离水面2米，已知水轮每分钟转动四圈，水轮上的点P相对于水面的高度y（米）与时间x（秒）满足函数关系y=Asin（ωx+φ）+B（A＞0，ω＞0，0＜φ＜2π），若x=0时，P在最高点，则函数表达式为：________．

    查看答案和解析>>

    科目：高中数学 来源：2010年湖北省襄樊四中高考数学模拟试卷（解析版） 题型：填空题

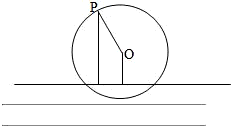
    如图，一个半径为10米的水轮按逆时针方向每分钟转4圈，记水轮上的点P到水面的距离为d米（P在水面下则d为负数），则d（米）与时间t（秒）之间满足关系式：d=Asin（ωt+φ）+k（A＞0，ω＞0），＜φ＜，且当P点从水面上浮现时开始计算时间，有以下四个结论：
    （1）A=10；
    （2）ω=；
    （3）φ=；
    （4）K=5，
    则其中所有正确结论的序号是    ．

    查看答案和解析>>

    同步练习册答案