
【题目】已知抛物线x2=2py(p>0),F为其焦点,过点F的直线l交抛物线于A、B两点,过点B作x轴的垂线,交直线OA于点C,如图所示.
(Ⅰ)求点C的轨迹M的方程;
(Ⅱ)直线m是抛物线的不与x轴重合的切线,切点为P,M与直线m交于点Q,求证:以线段PQ为直径的圆过点F.
【答案】解:(Ⅰ)由题意可得:直线l的斜率存在,设方程为:y=kx+ ![]() , 设A(x1 , y1),B(x2 , y2),动点C(x,y),
, 设A(x1 , y1),B(x2 , y2),动点C(x,y),
由 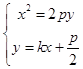 ,可得x2﹣2pkx﹣p2=0.可得x1x2═﹣p2 .
,可得x2﹣2pkx﹣p2=0.可得x1x2═﹣p2 .
OA:y= ![]() =
= ![]() ;OB:x=x2;
;OB:x=x2;
由  可得y=
可得y= ![]() ,
,
即点C的轨迹方程为y=﹣ ![]() .
.
(Ⅱ)证明:设直线m的方程为:y=kx+m,
由 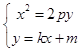 可得x2﹣2pkx﹣2pm=0可得△=4p2k2+8pm,因为直线m与抛物线相切,
可得x2﹣2pkx﹣2pm=0可得△=4p2k2+8pm,因为直线m与抛物线相切,
∴△=0,可得pk2+2m=0,可得P(pk,﹣m),
又由 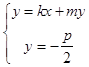 ,可得Q(
,可得Q( ![]() ),
),![]() =(pk,﹣m﹣
=(pk,﹣m﹣ ![]() )(
)( ![]() )
)
=﹣ ![]() (p+2m)+pm+
(p+2m)+pm+ ![]() =0,可得FP⊥FQ,
=0,可得FP⊥FQ,
∴以线段PQ为直径的圆过点F
【解析】(Ⅰ)判断直线l的斜率存在,设方程为:y=kx+ ![]() ,设A(x1 , y1),B(x2 , y2),动点C(x,y)联立直线与抛物线的方程组,利用韦达定理可得x1x2═﹣p2 . 求出OA;OB方程;然后求解轨迹方程.(Ⅱ)设直线m的方程为:y=kx+m,由
,设A(x1 , y1),B(x2 , y2),动点C(x,y)联立直线与抛物线的方程组,利用韦达定理可得x1x2═﹣p2 . 求出OA;OB方程;然后求解轨迹方程.(Ⅱ)设直线m的方程为:y=kx+m,由 ![]() ,得△=4p2k2+8pm,利用直线m与抛物线相切,得P(pk,﹣m),求出Q(
,得△=4p2k2+8pm,利用直线m与抛物线相切,得P(pk,﹣m),求出Q( ![]() ),通过
),通过 ![]() =0,说明以线段PQ为直径的圆过点F.
=0,说明以线段PQ为直径的圆过点F.


科目:高中数学 来源: 题型:
【题目】在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:
(Ⅰ)该顾客中奖的概率;
(Ⅱ)该顾客获得的奖品总价值ξ(元)的概率分布列和期望Eξ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=cos(2x﹣ ![]() )+2cos2x,将函数y=f(x)的图象向右平移
)+2cos2x,将函数y=f(x)的图象向右平移 ![]() 个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
个单位,得到函数y=g(x)的图象,则函数y=g(x)图象的一个对称中心是( )
A.(﹣ ![]() ,1)
,1)
B.(﹣ ![]() ,1)
,1)
C.( ![]() ,1)
,1)
D.( ![]() ,0)
,0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1、F2为双曲线的焦点,过F2垂直于实轴的直线交双曲线于A、B两点,BF1交y轴于点C,若AC⊥BF1 , 则双曲线的离心率为( )
A.![]()
B.![]()
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() (a>b>0)短轴的端点P(0,b)、Q(0,﹣b),长轴的一个端点为M,AB为经过椭圆中心且不在坐标轴上的一条弦,若PA、PB的斜率之积等于﹣
(a>b>0)短轴的端点P(0,b)、Q(0,﹣b),长轴的一个端点为M,AB为经过椭圆中心且不在坐标轴上的一条弦,若PA、PB的斜率之积等于﹣ ![]() ,则P到直线QM的距离为
,则P到直线QM的距离为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品计划提价,现有四种方案,方案(Ⅰ)先提价m%,再提价n%;方案(Ⅱ)先提价n%,再提价m%;方案(Ⅲ)分两次提价,每次提价( ![]() )%;方案(Ⅳ)一次性提价(m+n)%,已知m>n>0,那么四种提价方案中,提价最多的是( )
)%;方案(Ⅳ)一次性提价(m+n)%,已知m>n>0,那么四种提价方案中,提价最多的是( )
A.Ⅰ
B.Ⅱ
C.Ⅲ
D.Ⅳ
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题为真命题的是( )
A.若 x>y>0,则 ln x+ln y>0
B.“φ= ![]() ”是“函数 y=sin(2x+φ) 为偶函数”的充要条件
”是“函数 y=sin(2x+φ) 为偶函数”的充要条件
C.?x0∈(﹣∞,0),使 3x0<4x0成立
D.已知两个平面α,β,若两条异面直线m,n满足m?α,n?β且 m∥β,n∥α,则α∥β
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com