
【题目】裴波那契数列(Fibonacci sequence )又称黄金分割数列,因为数学家列昂纳多·裴波那契以兔子繁殖为例子引入,故又称为“兔子数列”,在数学上裴波那契数列被以下递推方法定义:数列![]() 满足:
满足:![]() ,
,![]() ,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
,现从该数列的前40项中随机抽取一项,则能被3整除的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】若A1,A2,…,Am为集合A={1,2,…,n}(n≥2且n∈N*)的子集,且满足两个条件:
①A1∪A2∪…∪Am=A;
②对任意的{x,y}A,至少存在一个i∈{1,2,3,…,m},使Ai∩{x,y}={x}或{y}.则称集合组A1,A2,…,Am具有性质P.
如图,作n行m列数表,定义数表中的第k行第l列的数为akl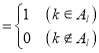 .
.
a11 | a12 | … | a1m |
a21 | a22 | … | a2m |
… | … | … | … |
an1 | an2 | … | anm |
(1)当n=4时,判断下列两个集合组是否具有性质P,如果是请画出所对应的表格,如果不是请说明理由;
集合组1:A1={1,3},A2={2,3},A3={4};
集合组2:A1={2,3,4},A2={2,3},A3={1,4}.
(2)当n=7时,若集合组A1,A2,A3具有性质P,请先画出所对应的7行3列的一个数表,再依此表格分别写出集合A1,A2,A3;
(3)当n=100时,集合组A1,A2,…,At是具有性质P且所含集合个数最小的集合组,求t的值及|A1|+|A2|+…|At|的最小值.(其中|Ai|表示集合Ai所含元素的个数)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于自然数数组![]() ,如下定义该数组的极差:三个数的最大值与最小值的差.如果
,如下定义该数组的极差:三个数的最大值与最小值的差.如果![]() 的极差
的极差![]() ,可实施如下操作
,可实施如下操作![]() :若
:若![]() 中最大的数唯一,则把最大数减2,其余两个数各增加1;若
中最大的数唯一,则把最大数减2,其余两个数各增加1;若![]() 中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为
中最大的数有两个,则把最大数各减1,第三个数加2,此为一次操作,操作结果记为![]() ,其级差为
,其级差为![]() .若
.若![]() ,则继续对
,则继续对![]() 实施操作
实施操作![]() ,…,实施
,…,实施![]() 次操作后的结果记为
次操作后的结果记为![]() ,其极差记为
,其极差记为![]() .例如:
.例如:![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)已知![]() 的极差为
的极差为![]() 且
且![]() ,若
,若![]() 时,恒有
时,恒有![]() ,求
,求![]() 的所有可能取值;
的所有可能取值;
(3)若![]() 是以4为公比的正整数等比数列中的任意三项,求证:存在
是以4为公比的正整数等比数列中的任意三项,求证:存在![]() 满足
满足![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,实数
,实数![]() 且
且![]() .
.
(1)设![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性,并说明理由;
上的单调性,并说明理由;
(2)设![]() 且
且![]() 时,
时,![]() 的定义域和值域都是
的定义域和值域都是![]() ,求
,求![]() 的最大值;
的最大值;
(3)若不等式![]() 对
对![]() 恒成立,求
恒成立,求![]() 的范围.
的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市在开展创建“全国文明城市”活动中,工作有序扎实,成效显著,尤其是城市环境卫生大为改观,深得市民好评.“创文”过程中,某网站推出了关于环境治理和保护问题情况的问卷调查,现从参与问卷调查的人群中随机选出200人,并将这200人按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.
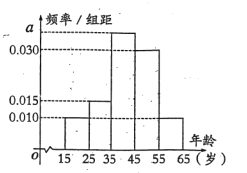
(1)求出a的值;
(2)若已从年龄较小的第1,2组中用分层抽样的方法抽取5人,现要再从这5人中随机抽取3人进行问卷调查,设第2组抽到![]() 人,求随机变量
人,求随机变量![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}中,相邻两项an,an+1是关于x的方程:x2+3nx+bn![]() 0(n∈N*)的两实根,且a1=1.
0(n∈N*)的两实根,且a1=1.
(1)若Sn为数列{an}的前n项和,求S100 ;
(2)求数列{an}和{bn}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,若在定义域内存在实数
,若在定义域内存在实数![]() ,满足
,满足![]() ,则称
,则称![]() 为“局部奇函数”.
为“局部奇函数”.
(1)已知二次函数![]() ,试判断
,试判断![]() 是否为“局部奇函数”?并说明理由;
是否为“局部奇函数”?并说明理由;
(2)若![]() 是定义在区间
是定义在区间![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 为定义域
为定义域![]() 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数![]() 的取值范围;
的取值范围;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com