练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （1）用反证法证明：在一个三角形中，至少有一个内角大于或等于60°.
    （2）已知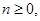试用分析法证明： .

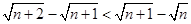    （1）先假设再根据三角形内角和定理即可得出矛盾.
    （2）按照分析法的一般步骤由要证结论出发，得出1>0，即得证.

    解析试题分析：（1）证明：假设在一个三角形中，没有一个内角大于或等于60°，
    即均小于60°，
    则三内角和小于180°，与三角形中三内角和等于180°矛盾，故假设不成立 .原命题成立 .
    （2）证明：要证上式成立，需证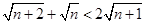    
    需证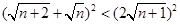          
    需证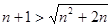                   
    需证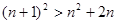    
    需证，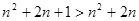            
    只需证1>0                               
    因为1>0显然成立，所以原命题成立 .  
    考点：反证法．
    点评：反证法的步骤是：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立．在假设结论不成立时，要注意考虑结论的反面所有可能的情况，如果只有一种，那么否定一种就可以了，如果有多种情况，则必须一一否定．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    5、（1）已知p3+q3=2，求证p+q≤2，用反证法证明时，可假设p+q≥2；
    （2）已知a，b∈R，|a|+|b|＜1，求证方程x2+ax+b=0的两根的绝对值都小于1．用反证法证明时可假设方程有一根x1的绝对值大于或等于1，即假设|x1|≥1，以下结论正确的是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=lg(
    2a1+x
    -1)    （其中a＞0）．求证：
    （1）用反证法证明函数f（x）不能为偶函数；
    （2）函数f（x）为奇函数的充要条件是a=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）用反证法证明：如果x＞
    1
    2
    ，那么x2+2x-1≠0；
    （2）用数学归纳法证明：
    1
    1×3
    +
    1
    3×5
    +…+
    1
    (2n-1)×(2n+1)
    =
    n
    2n+1
    (n∈N*)    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）用反证法证明：在一个三角形中，至少有一个内角大于或等于60°．
    （2）已知n≥0，试用分析法证明：
    		n+2
    -
    		n+1
    ＜
    		n+1
    -
    		n
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （1）求证：
    		7
    -
    		6
    ＜
    		5
    -2    ；
    （2）已知函数f（x）=ex+
    x-2
    x+1
    ，用反证法证明方程f（x）=0没有负数根．

    查看答案和解析>>

    同步练习册答案