
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,集合
,集合![]() ,集合B={
,集合B={![]()
![]() x2﹣y2=1,x,y∈R},请判断下列三个命题的真假.若为真,请给予证明;若为假,请举出反例.
x2﹣y2=1,x,y∈R},请判断下列三个命题的真假.若为真,请给予证明;若为假,请举出反例.
(1)以集合![]() 中的元素为坐标的点均在同一条直线上;
中的元素为坐标的点均在同一条直线上;
(2)A∩B至多有一个元素;
(3)当a1≠0时,一定有A∩B≠..
【答案】(1)真命题,点(an,![]() )均在直线y=
)均在直线y=![]() x+
x+![]() a1上,见解析;(2)真命题,见解析;(3)假命题,见解析
a1上,见解析;(2)真命题,见解析;(3)假命题,见解析
【解析】
(1)在等差数列中,写出数列的前n项和的公式,表达出集合中的元素,得到点的坐标适合直线的方程.
(2)列出方程组,利用消元法求出方程组的解,验证这个方程组只有一个解,得到这个集合至多有一个元素.
(3)验证当首项为1,公差为1时,集合A中的元素作为点的坐标,其横、纵坐标均为正,由于a1=1≠0,如果A∩B≠,根据(2)的结论,A∩B至多有一个元素(x0,y0),当a1≠0时,一定有A∩B≠是不正确的.
(1)在等差数列{an}中,对一切n∈N*,有Sn=![]() ,则
,则![]() ,
,
这表明点(an,![]() )适合方程y=
)适合方程y=![]() (x+a1),于是点(an,
(x+a1),于是点(an,![]() )均在直线y=
)均在直线y=![]() x+
x+![]() a1上.
a1上.
(2)设(x,y)∈A∩B,则x,y是方程组 的解,
的解,
由方程组消去y得2a1x+a12=﹣4,
当a1=0时,方程2a1x+a12=﹣4无解,此时A∩B=;
当a1≠0时,方程2a1x+a12=﹣4只有一个解x=![]() ,此时,方程组只有一解,
,此时,方程组只有一解,
故上述方程组至多有解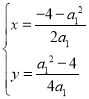 ,∴A∩B至多有一个元素.
,∴A∩B至多有一个元素.
(3)取a1=1,d=1,对一切的n∈N*,有an=a1+(n﹣1)d=n>0,![]() >0,
>0,
这时集合A中的元素作为点的坐标,其横、纵坐标均为正,另外,由于a1=1≠0,如果A∩B≠,
那么根据(2)的结论,A∩B至多有一个元素(x0,y0),
而x0=![]() =﹣
=﹣![]() <0,y0=
<0,y0=![]() =﹣
=﹣![]() <0,这样的(x0,y0)A,产生矛盾,故a1=1,d=1时,A∩B=,
<0,这样的(x0,y0)A,产生矛盾,故a1=1,d=1时,A∩B=,
∴当a1≠0时,一定有A∩B≠是不正确的.


科目:高中数学 来源: 题型:
【题目】一布袋中装有![]() 个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
个小球,甲,乙两个同学轮流且不放回的抓球,每次最少抓一个球,最多抓三个球,规定:由乙先抓,且谁抓到最后一个球谁赢,那么以下推断中正确的是( )
A. 若![]() ,则乙有必赢的策略B. 若
,则乙有必赢的策略B. 若![]() ,则甲有必赢的策略
,则甲有必赢的策略
C. 若![]() ,则甲有必赢的策略D. 若
,则甲有必赢的策略D. 若![]() ,则乙有必赢的策略
,则乙有必赢的策略
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划购买1台机器,该种机器使用三年后即被淘汰.在购进机器时,可以一次性额外购买几次维修服务,每次维修服务费用200元,另外实际维修一次还需向维修人员支付小费,小费每次50元.在机器使用期间,如果维修次数超过购机时购买的维修服务次数,则每维修一次需支付维修服务费用500元,无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务,为此搜集并整理了100台这种机器在三年使用期内的维修次数,得下面统计表:
维修次数 | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 20 | 30 | 30 | 10 |
记x表示1台机器在三年使用期内的维修次数,y表示1台机器在维修上所需的费用(单位:元),![]() 表示购机的同时购买的维修服务次数.
表示购机的同时购买的维修服务次数.
(1)若![]() =10,求y与x的函数解析式;
=10,求y与x的函数解析式;
(2)若要求“维修次数不大于![]() ”的频率不小于0.8,求n的最小值;
”的频率不小于0.8,求n的最小值;
(3)假设这100台机器在购机的同时每台都购买10次维修服务,或每台都购买11次维修服务,分别计算这100台机器在维修上所需费用的平均数,以此作为决策依据,购买1台机器的同时应购买10次还是11次维修服务?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在图1所示的梯形![]() 中,
中,![]() ,
,![]() 于点
于点![]() ,且
,且![]() .将梯形
.将梯形![]() 沿
沿![]() 对折,使平面
对折,使平面![]() 平面
平面![]() ,如图2所示,连接
,如图2所示,连接![]() ,取
,取![]() 的中点
的中点![]() .
.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得直线
,使得直线![]() 平面
平面![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置,并给予证明;若不存在,请说明理由;
的位置,并给予证明;若不存在,请说明理由;
(3)设![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com