
【题目】2016年高一新生入学后,为了了解新生学业水平,某区对新生进行了水平测试,随机抽取了50名新生的成绩,其相关数据统计如下:
分数段 | 频数 | 选择题得分24分以上(含24分) |
| 5 | 2 |
| 10 | 4 |
| 15 | 12 |
| 10 | 6 |
| 5 | 4 |
| 5 | 5 |
(Ⅰ)若从分数在![]() ,
, ![]() 的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
的被调查的新生中各随机选取2人进行追踪调查,求恰好有2名新生选择题得分不足24分的概率;
(Ⅱ)在(Ⅰ)的条件下,记选中的4名新生中选择题得分不足24分的人数为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知Sn为公差不为0的等差数列{an}的前n项和,且a1=1,S1 , S2 , S4成等比数列.
(1)求数列{an}的通项公式;
(2)设 ![]() ,求数列{bn}的前n项和.
,求数列{bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的前n项和为Sn , 已知a3=3,S11=0.
(1)求数列{an}的通项公式;
(2)当n为何值时,Sn最大,并求Sn的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有两个袋子,其中甲袋中装有编号分别为1、2、3、4的4个完全相同的球,乙袋中装有编号分别为2、4、6的3个完全相同的球.
(Ⅰ)从甲、乙袋子中各取一个球,求两球编号之和小于8的概率;
(Ⅱ)从甲袋中取2个球,从乙袋中取一个球,求所取出的3个球中含有编号为2的球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣ ![]() ,0),B(
,0),B( ![]() ,0),动点E满足直线EA与直线EB的斜率之积为﹣
,0),动点E满足直线EA与直线EB的斜率之积为﹣ ![]() .
.
(1)求动点E的轨迹C的方程;
(2)设过点F(1,0)的直线l1与曲线C交于点P,Q,记点P到直线l2:x=2的距离为d. 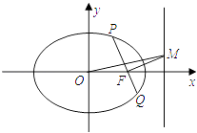
(ⅰ)求 ![]() 的值;
的值;
(ⅱ)过点F作直线l1的垂线交直线l2于点M,求证:直线OM平分线段PQ.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,在边长为3的正三角形中, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 上的点,且满足
上的点,且满足![]() .将
.将![]() 沿
沿![]() 折起到
折起到![]() 的位置,使平面
的位置,使平面![]() 平面
平面![]() ,连结
,连结![]() ,
, ![]() ,
, ![]() .(如图2)
.(如图2)
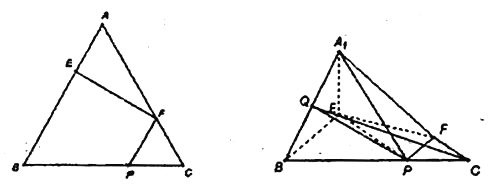
(Ⅰ)若![]() 为
为![]() 中点,求证:
中点,求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ;
;
(Ⅲ)求![]() 与平面
与平面![]() 所成角的正切.
所成角的正切.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知⊙O:x2+y2=1和定点A(2,1),由⊙O外一点P(a,b)向⊙O引切线PQ,切点为Q,且满足|PQ|=|PA|.
(1)求实数a,b间满足的等量关系;
(2)求线段PQ长的最小值;
(3)若以P为圆心所作的⊙P与⊙O有公共点,试求半径最小值时⊙P的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如下.则下面结论中错误的一个是( ) 
A.甲的极差是29
B.乙的众数是21
C.甲罚球命中率比乙高
D.甲的中位数是24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com