
【题目】已知函数f(x)=|ax2+x﹣4a|,其中x∈[﹣2,2],a∈[﹣1,1].
(1)当α=1时,求函数y=f(x)的值域;
(2)记f(x)的最大值为M(a),求M(a)的取值范围.
【答案】
(1)解:当α=1时,f(x)=|x2+x﹣4|,x∈[﹣2,2],
由x2+x﹣4=0,解得x= ![]() ,
,
由f(x)在[﹣2,﹣ ![]() ]递增,在(﹣
]递增,在(﹣ ![]() ,
, ![]() )递减,
)递减,
在( ![]() ,2]递增,可得
,2]递增,可得
f(x)的最小值为0,由f(﹣ ![]() )=
)= ![]() ,f(2)=4,
,f(2)=4,
最大值为 ![]() .
.
则f(x)的值域为[0, ![]() ];
];
(2)解:设f(x)=0的两根为x1,x2,(x1<x2),
当﹣1≤a≤﹣ ![]() 时,f(x)在(﹣2,x1)递减,(x1,﹣
时,f(x)在(﹣2,x1)递减,(x1,﹣ ![]() )递增,(﹣
)递增,(﹣ ![]() ,2)递减,
,2)递减,
可得f(x)在x=﹣ ![]() 处取得最大值,且为﹣
处取得最大值,且为﹣ ![]() ;
;
当﹣ ![]() <a≤0时,f(x)在(﹣2,x1)递减,(x1,2)递增,
<a≤0时,f(x)在(﹣2,x1)递减,(x1,2)递增,
可得f(x)在x=±2处取得最大值2;
当0<a≤ ![]() 时,f(x)在(﹣2,x2)递减,(x2,2)递增,可得f(x)在x=±2处取得最大值2;
时,f(x)在(﹣2,x2)递减,(x2,2)递增,可得f(x)在x=±2处取得最大值2;
当 ![]() <a≤1时,f(x)在(﹣2,﹣
<a≤1时,f(x)在(﹣2,﹣ ![]() )递增,(﹣
)递增,(﹣ ![]() ,x2)递减,(x2,2)递增,
,x2)递减,(x2,2)递增,
可得f(x)在x=﹣ ![]() 处取得最大值,且为
处取得最大值,且为 ![]() .
.
即有M(a)= 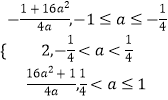 ,
,
当﹣1≤a≤﹣ ![]() 时,M(a)=(﹣4a)+
时,M(a)=(﹣4a)+ ![]() 在[﹣1,﹣
在[﹣1,﹣ ![]() ]递减,可得M(a)∈[2,
]递减,可得M(a)∈[2, ![]() ];
];
当 ![]() <a≤1时,M(a)=4a+
<a≤1时,M(a)=4a+ ![]() 递增,可得M(a)∈[2,
递增,可得M(a)∈[2, ![]() ].
].
综上可得,M(a)的取值范围是[2, ![]() ]
]
【解析】(1)求出当α=1时,f(x)=|x2+x﹣4|,x∈[﹣2,2],解方程可得两根,再由f(x)的单调性,可得值域;(2)设f(x)=0的两根为x1 , x2 , (x1<x2),对a讨论,当﹣1≤a≤﹣ ![]() 时,当﹣
时,当﹣ ![]() <a≤0时,当0<a≤
<a≤0时,当0<a≤ ![]() 时,当
时,当 ![]() <a≤1时,运用单调性可得最大值,再由基本不等式和单调性,即可得到所求范围.
<a≤1时,运用单调性可得最大值,再由基本不等式和单调性,即可得到所求范围.
【考点精析】掌握二次函数的性质和绝对值不等式的解法是解答本题的根本,需要知道当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.
上递减;含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() 右支上非顶点的一点A关于原点O的对称点为B,F为其右焦点,若AF⊥FB,设∠ABF=θ且
右支上非顶点的一点A关于原点O的对称点为B,F为其右焦点,若AF⊥FB,设∠ABF=θ且 ![]() ,则双曲线离心率的取值范围是( )
,则双曲线离心率的取值范围是( )
A.![]()
B.![]()
C.![]()
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分)
,现有一组数据(数据量较大),从中随机抽取10个,绘制所得的茎叶图如图所示,且茎叶图中的数据的平均数为2.(茎叶图中的数据均为小数,其中茎为整数部分,叶为小数部分) 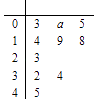
(Ⅰ)现从茎叶图的数据中任取4个数据分别替换m的值,
求至少有2个数据使得函数f(x)没有零点的概率;
(Ⅱ)以频率估计概率,若从该组数据中随机抽取4个数据分别替换m的值,记使得函数f(x)没有零点的个数为ξ,求ξ的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C在直角坐标系xOy下的参数方程为 ![]() (θ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(θ为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求曲线C的极坐标方程;
(2)直线l的极坐标方程是ρcos(θ﹣ ![]() )=3
)=3 ![]() ,射线OT:θ=
,射线OT:θ= ![]() (ρ>0)与曲线C交于A点,与直线l交于B,求线段AB的长.
(ρ>0)与曲线C交于A点,与直线l交于B,求线段AB的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的图象上存在两点,使得函数的图象在这两点处的切线互相垂直,则称y=f(x)具有T性质.下列函数中具有T性质的是( )
A.y=sinx
B.y=lnx
C.y=ex
D.y=x3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com