
(Ⅰ)求甲射击4次,至少有1次未击中目标的概率;
(Ⅱ)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(Ⅲ)假设某人连续2次未击中目标,则中止其射击.问:乙恰好射击5次后,被中止射击的概率是多少?
(20)解:(Ⅰ)记“甲连续射击4次至少有1次未击中目标”为事件A1,由题意,射击4次,相当于作4次独立重复试验,故
P(A1)=1-P(![]() )=1-(
)=1-(![]() )4=
)4=![]() .
.
答:甲连续射击4次至少有1次未击中目标的概率为![]() .
.
(Ⅱ)记“甲射击4次,恰有2次击中目标”为事件A2,“乙射击4次,恰有3次击中目标”为事件B2,则
P(A2)=C![]() ×(
×(![]() )2×(1-
)2×(1-![]() )4-2=
)4-2=![]() ,
,
P(B2)=C![]() ×(
×(![]() )3×(1-
)3×(1-![]() )4-3=
)4-3=![]() 。
。
由于甲、乙射击相互独立,故
P(A2B2)=P(A2)P(B2)=![]() ×
×![]() =
=![]() 。
。
答:两人各射击4次,甲恰有2次击中目标且乙恰有3次击中目标的概率为![]() 。
。
(Ⅲ)记“乙恰好射击5次后被中止射击”为事件A3,“乙第i次射击未击中”为事件Di(i=1,2,3,4,5),则A3=D5D4![]() (
(![]() ),且P(Di)=
),且P(Di)=![]() 。由于各事件相互独立,故
。由于各事件相互独立,故
P(A3)=P(D5)P(D4)P(![]() )P(
)P(![]() )
)
=![]() .
.
答:乙恰好射击5次后被中止射击的概率为![]() 。
。


科目:高中数学 来源: 题型:
 20、如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:
20、如图,A地到火车站共有两条路径L1和L2,现随机抽取100位从A地到火车站的人进行调查,调查结果如下:| 所用时间(分钟) | 10~20 | 20~30 | 30~40 | 40~50 | 50~60 |
| 选择L1的人数 | 6 | 12 | 18 | 12 | 12 |
| 选择L2的人数 | 0 | 4 | 16 | 16 | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2013•牡丹江一模)某大学高等数学老师这学期分别用A,B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:
(2013•牡丹江一模)某大学高等数学老师这学期分别用A,B两种不同的教学方式试验甲、乙两个大一新班(人数均为60人,入学数学平均分数和优秀率都相同;勤奋程度和自觉性都一样).现随机抽取甲、乙两班各20名的高等数学期末考试成绩,得到茎叶图:| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
查看答案和解析>>
科目:高中数学 来源: 题型:044
(2005
江苏,20)甲、乙两人各射击1次,击中目标的概率分别是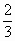 和
和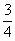 .假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)
求甲射击4次,至少有1次未击中目标的概率;(2)
求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;(3)
假设某人连续2次未击中目标,则中止其射击.问:乙恰好射击5次后,被中止射击的概率是多少?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com