练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】等差数列{an}中的a2、a4032是函数 的两个极值点，则log2（a2a2017a4032）=（　　）
    A.
    B.4
    C.
    D.

    【答案】C
    【解析】解：∵ ，

    ∴f′（x）=x2﹣8x+6，

    ∵等差数列{an}中的a2、a4032是函数 的两个极值点，

    ∴a2+a4032=8，a2a4032=6，

    ∴ =4，

    ∴log2（a2a2017a4032）=log2（4×6）= =3+log23．

    故选：C．

    【考点精析】本题主要考查了函数的极值与导数和等差数列的通项公式（及其变式）的相关知识点，需要掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值；通项公式：或才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】《九章算术》是我国古代的数学名著，体现了古代劳动人民的数学智慧，其中第六章“均输”中，有一竹节容量问题，某人根据这一思想，设计了如图所示的程序框图，若输出m的值为35，则输入的a的值为 ．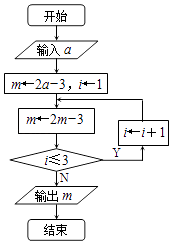

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】运行如图所示的流程图，则输出的结果S是（　　）

    A.
    B.
    C.﹣1
    D.1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点（2，3）在椭圆 上，设A，B，C分别为椭圆的左顶点、上顶点、下顶点，且点C到直线AB的距离为 ．
    （I）求椭圆C的方程；
    （II）设M（x1 ， y1），N（x2 ， y2）（x1≠x2）为椭圆上的两点，且满足 = ，求证：△MON的面积为定值，并求出这个定值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱柱ABC﹣A1B1C1中，AB=BC=CA=AA1=2，侧棱AA1⊥平面ABC，且D，E分别是棱A1B1 ， A1A1的中点，点F在棱AB上，且AF= AB．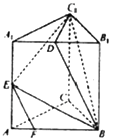

    （1）求证：EF∥平面BDC1；
    （2）求三棱锥D﹣BEC1的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知D是直角ABC斜边BC上一点，AC= DC，
    （Ⅰ）若∠DAC=30°求角B的大小；
    （Ⅱ）若BD=2DC，且 AD=2 ，求DC的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知抛物线y2=2px（p＞0），过点C（﹣4，0）作抛物线的两条切线CA，CB，A，B为切点，若直线AB经过抛物线y2=2px的焦点，△CAB的面积为24，则以直线AB为准线的抛物线标准方程是（　　）
    A.y2=4x
    B.y2=﹣4x
    C.y2=8x
    D.y2=﹣8x

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系xOy中，已知点P（1，﹣2），直线l： （m 为参数），以坐标原点为极点，以 x轴的正半轴为极轴建立极坐标系；曲线C的极坐标方程为ρsin2θ=3cosθ；直线l与曲线C的交点为A，B．
    （1）求直线l和曲线C的普通方程；
    （2）求 + 的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知各项均为整数的数列{an}中，a1=2，且对任意的n∈N* ， 满足an+1﹣an＜2n+ ﹣1，则a2017= ．

    查看答案和解析>>

    同步练习册答案