练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某保险公司利用简单随机抽样方法，对投保车辆进行抽样，样本车辆中每辆车的赔付结果统计如下：

    赔付金额（元）
    		0
    		1000
    		2000
    		3000
    		4000
    车辆数（辆）
    		500
    		130
    		100
    		150
    		120
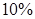    （1）若每辆车的投保金额均为2800元，估计赔付金额大于投保金额的概率；
    （2）在样本车辆中，车主是新司机的占，在赔付金额为4000元的样本车辆中，车主是新司机的占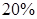，（3）估计在已投保车辆中，新司机获赔金额为4000元的概率.

    （1）0.27；（2）0.24.

    解析试题分析：（1）设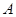表示事件“赔付金额为3000元”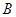，表示事件“赔付金额为4000元”，以频率估计概率求得，，在根据投保金额为2800，赔付金额大于投保金额对应的情形时3000元和4000元，问题就得以解决；
    （2）设表示事件“投保车辆中新司机获赔4000元”，分别求出样本车辆中车主为新司机人数和赔付金额为4000元的车辆中车主为新司机人数，在求出其频率，最后利用频率表示概率.
    试题解析：
    （1）设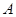表示事件“赔付金额为3000元”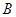，表示事件“赔付金额为4000元”，以频率估计概率得：
    ，，
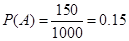    由于投保金额为2800，赔付金额大于投保金额对应的情形时3000元和4000元，所以其概率为：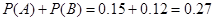

    设表示事件“投保车辆中新司机获赔4000元”，由已知，样本车辆中车主为新司机的有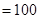，而赔付金额为4000元的车辆中车主为新司机的有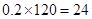
    所以样本中车辆中新司机车主获赔金额为4000元的频率为
    由频率估计概率得
    考点：古典概型及其概率计算公式.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    设有关于x的一元二次方程x2+2ax+b2="0." (l)若a是从0,1,2,3四个数中任取的一个数，b是从0,1,2三个数中任取的一个数，求方程有实根的概率；(2)若a是从区间[0，t+1]任取的一个数，b是从区间[0,t]任取的一个数，其中t满足2≤t≤3，求方程有实根的概率，并求出其概率的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    假设某班级教室共有4扇窗户，在每天上午第三节课上课预备铃声响起时，每扇窗户或被敞开或被关闭，且概率均为0.5.记此时教室里敞开的窗户个数为X.
    (1)求X的分布列；
    (2)若此时教室里有两扇或两扇以上的窗户被关闭，班长就会将关闭的窗户全部敞开，否则维持原状不变．记每天上午第三节课上课时该教室里敞开的窗户个数为Y，求Y的数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某花店每天以每枝5元的价格从农场购进若干枝玫瑰花，然后以每枝10元的价格出售．如果当天卖不完，剩下的玫瑰花作垃圾处理．
    (1)若花店一天购进17枝玫瑰花，求当天的利润y(单位：元)关于当天需求量n(单位：枝，n∈N)的函数解析式；
    (2)花店记录了100天玫瑰花的日需求量(单位：枝)，整理得下表：

    日需求量n
    		14
    		15
    		16
    		17
    		18
    		19
    		20
    频数
    		10
    		20
    		16
    		16
    		15
    		13
    		10
     
    ①假设花店在这100天内每天购进17枝玫瑰花，求这100天的日利润(单位：元)的平均数；
    ②若花店一天购进17枝玫瑰花，以100天记录的各需求量的频率作为各需求量发生的概率，求当天的利润不少于75元的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某学校高一年级组建了A、B、C、D四个不同的“研究性学习”小组，要求高一年级学生必须参加，
    且只能参加一个小组的活动．假定某班的甲、乙、丙三名同学对这四个小组的选择是等可能的.
    （1）求甲、乙、丙三名同学选择四个小组的所有选法种数；
    （2）求甲、乙、丙三名同学中至少有二人参加同一组活动的概率；
    （3）设随机变量X为甲、乙、丙三名同学参加A小组活动的人数，求X的分布列与数学期望EX．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中，随机抽取了100名电视观众，相关的数据如下表所示：

     
    		文艺节目
    		新闻节目
    		总计
    20至40岁
    		40
    		18
    		58
    大于40岁
    		15
    		27
    		42
    总计
    		55
    		45
    		100
     
    (1)由表中数据直观分析，收看新闻节目的观众是否与年龄有关？
    (2)用分层抽样方法在收看新闻节目的观众中随机抽取5名，大于40岁的观众应该抽取几名？
    (3)在上述抽取的5名观众中任取2名，求恰有1名观众的年龄为20至40岁的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    随机观测生产某种零件的某工厂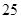名工人的日加工零件数（单位：件），获得数据如下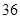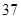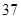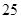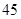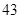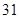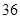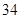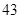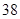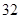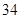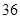：、、、、、、、、、、、、、、、、、、、、、、、、，根据上述数据得到样本的频率分布表如下：

    分组
    		频数
    		频率















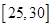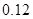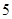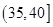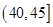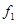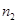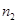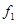    （1）确定样本频率分布表中、、和的值；
    （2）根据上述频率分布表，画出样本频率分布直方图；
    （3）根据样本频率分布直方图，求在该厂任取人，至少有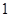人的日加工零件数落在区间的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

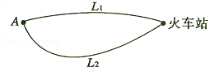
    （13分）（2011•陕西）如图，A地到火车站共有两条路径L1和L2，现随机抽取100位从A地到火车站的人进行调查，调查结果如下：

    所用时间（分钟）
    		10～20
    		20～30
    		30～40
    		40～50
    		50～60
    选择L1的人数
    		6
    		12
    		18
    		12
    		12
    选择L2的人数
    		0
    		4
    		16
    		16
    		4

    （Ⅰ）试估计40分钟内不能         赶到火车站的概率；
    （Ⅱ）分别求通过路径L1和L2所用时间落在上表中各时间段内的频率；
    （Ⅲ）现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站，为了尽量大可能在允许的时间内赶到火车站，试通过计算说明，他们应如何选择各自的 路径．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    近年空气质量逐步恶化，雾霾天气现象出现增多，大气污染危害加重，大气污染可引起心悸、呼吸困难等心肺疾病．为了解某市心肺疾病是否与性别有关，在某医院随机对入院的50人进行了问卷调查得到了如下的列联表：

     
    		患心肺疾病
    		不患心肺疾病
    		合计
    男
    		 
    		5
    		 
    女
    		10
    		 
    		 
    合计
    		 
    		 
    		50
     
    已知在全部50人中随机抽取1人，抽到患心肺疾病的人的概率为．
    (1)请将上面的列联表补充完整；
    (2)是否有99．5%的把握认为患心肺疾病与性别有关？说明你的理由；
    临界值表供参考：
    P(K2≥k)
    		0．15
    		0．10
    		0．05
    		0．025
    		0．010
    		0．005
    		0．001
    k
    		2．072
    		2．706
    		3．841
    		5．024
    		6．635
    		7．879
    		10．828
     
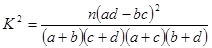    参考公式：其中

    查看答案和解析>>

    同步练习册答案