
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
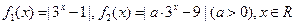 ,
, 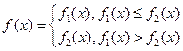 .
.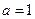 时,求
时,求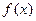 在
在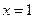 处的切线方程;
处的切线方程;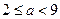 时,设
时,设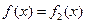 所对应的自变量取值区间的长度为
所对应的自变量取值区间的长度为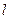 (闭区间
(闭区间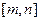 的长度定义为
的长度定义为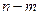 ),试求
),试求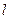 的最大值;
的最大值;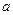 ,使得当
,使得当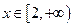 时,
时,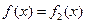 ?若存在,求出
?若存在,求出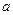 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.汽车的行驶公里数与耗油量的关系 |
| B.我国人口自然增长率为1%,这样我国人口总数随年份的变化关系 |
| C.竖直向上发射的信号弹,从发射到落回地面时,信号弹的高度与时间的关系(不计空气阻力) |
| D.核电站中,作为核燃料的某放射元素裂变后,所剩原子数随使用时间的变化关系 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com