
分析 (1)过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,根据角平分线上的点到角的两边的距离相等可得DE=DF,然后根据三角形的面积公式列式即可求出两三角形的面积的比值.
(2)利用已知及倍角公式可求cosB,即可求得sinB,sinC,cosC,cosA的值,进而可求sin∠BAD=sin$\frac{A}{2}$,由正弦定理可求得BD=$\frac{AD×sin∠BAD}{sinB}$=3,可求ED,BE,AE的值,求得S△ABD,S△ACD,即可得解△ABC的面积.
解答 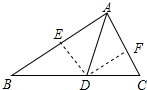 解:(1)如图,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
解:(1)如图,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F,
∵AD是△ABC的角平分线,
∴DE=DF,
∴S△ABD=$\frac{1}{2}$AB•DE,S△ACD=$\frac{1}{2}$AC•DF,
∵△ABD的面积与△ACD的面积比为3:2.
∴S△ABD:S△ACD=($\frac{1}{2}$AB•DE):($\frac{1}{2}$AC•DF)=AB:AC=3:2,解得:$\frac{AB}{AC}$=$\frac{3}{2}$,
∴利用正弦定理及比例的性质可得:$\frac{sinB}{sinC}$=$\frac{AC}{AB}=\frac{2}{3}$.
(2)∵C=2B,即,sinC=sin2B=2sinBcosB,又$\frac{sinB}{sinC}$=$\frac{2}{3}$,即sinC=$\frac{3sinB}{2}$,
∴2sinBcosB=$\frac{3sinB}{2}$,B为锐角,解得:cosB=$\frac{3}{4}$,
∴可得sinB=$\frac{\sqrt{7}}{4}$,sinC=$\frac{3\sqrt{7}}{8}$,cosC=cos2B=2cos2B-1=$\frac{1}{8}$,
∴cosA=-cos(B+C)=-(cosBcosC-sinBsinC)=-($\frac{3}{4}×\frac{1}{8}$-$\frac{\sqrt{7}}{4}$×$\frac{3\sqrt{7}}{8}$)=$\frac{9}{16}$,
∴sin∠BAD=sin$\frac{A}{2}$=$\sqrt{\frac{1-cosA}{2}}$=$\frac{\sqrt{14}}{8}$,
∴在△ABD中,由正弦定理可得:BD=$\frac{AD×sin∠BAD}{sinB}$=$\frac{3\sqrt{2}×\frac{\sqrt{14}}{8}}{\frac{\sqrt{7}}{4}}$=3.
∴△BDE中,ED=BDsinB=3×$\frac{\sqrt{7}}{4}$=$\frac{3\sqrt{7}}{4}$.
∴BE=BDcosB=3×$\frac{3}{4}$=$\frac{9}{4}$,
AE=$\sqrt{A{D}^{2}-E{D}^{2}}$=$\sqrt{(3\sqrt{2})^{2}-(\frac{3\sqrt{7}}{4})^{2}}$=$\frac{15}{4}$,
∴S△ABD=$\frac{1}{2}$×AB×ED=$\frac{1}{2}×$(AE+BE)×ED=$\frac{1}{2}×$($\frac{15}{4}$+$\frac{9}{4}$)×$\frac{3\sqrt{7}}{4}$=$\frac{9\sqrt{7}}{4}$,S△ACD=$\frac{3\sqrt{7}}{2}$,
∴△ABC的面积=S△ABD+S△ACD=$\frac{9\sqrt{7}}{4}$+$\frac{3\sqrt{7}}{2}$=$\frac{15\sqrt{7}}{4}$.
点评 本题主要考查了角平分线上的点到角的两边的距离相等的性质,考查了三角形的面积公式,正弦定理,同角三角函数基本关系式的应用,作出辅助线表示出三角形的面积是解题的关键,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| 酒驾人数x | 80 | 147 | 121 | 100 | 96 | 103 | 87 |
| 交通事故y | 19 | 31 | 30 | 23 | 25 | 24 | 20 |
| A. | 正相关 | B. | 负相关 | C. | 不相关 | D. | 函数关系 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com