解:(1)解|x-1|≥1得:x≤0或x≥2∴A={x|x≤0,或x≥2};
∵函数f(x)的自变量x应满足
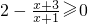
,即
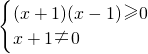
∴x<-1或x≥1∴B={x|x<-1,或x≥1};
A∩B={x|x<-1,或x≥2},
A∪B={x|x≤0,或x≥1},
C
U(A∪B)={x|0<x<1}
(2)∵函数g(x)的自变量x应满足不等式(x-a-1)(2a-x)>0.
又由a<1,∴2a<x<a+1∴C={x|2a<x<a+1}
∵C⊆B∴a+1≤-1或2a≥1∴a≤-2或

,
又a<1∴a的取值范围为a≤-2或
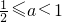
.
分析:(1)根据含有绝对值不等式的解法求得集合A,根据偶次开方的被开方数为非负得到B,可以求出集合A∩B;C
U(A∪B);
(2)先对集合C进行曲化简,函数g(x)的自变量x应满足不等式(x-a-1)(2a-x)>0即C={x|2a<x<a+1},根据集合C是集合B的子集,即可求出a的范围;
点评:本题主要考查了集合交集、补集运算,以及集合的包含关系判断及应用,解决此题的关键是不等式的解法及集合间的交、并、补运算,是高考中的常考内容,要引起注意.

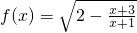 的定义域,C为g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域;
的定义域,C为g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域;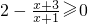 ,即
,即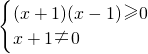
 ,
,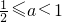 .
.

 同步练习强化拓展系列答案
同步练习强化拓展系列答案