
【题目】已知椭圆![]() 的离心率
的离心率![]() ,过点
,过点![]() 的直线与原点的距离为
的直线与原点的距离为![]() .
.
(1)求椭圆方程;
(2)若直线![]() 与椭圆交于
与椭圆交于![]() 两点,试求
两点,试求![]() 面积的范围.
面积的范围.
科目:高中数学 来源: 题型:
【题目】给出下列结论:
①“![]() 且
且![]() 为真”是“
为真”是“![]() 或
或![]() 为真”的充分不必要条件:②“
为真”的充分不必要条件:②“![]() 且
且![]() 为假”是“
为假”是“![]() 或
或![]() 为真”的充分不必要条件;③“
为真”的充分不必要条件;③“![]() 或
或![]() 为真”是“非
为真”是“非![]() 为假”的必要不充分条件;④“非
为假”的必要不充分条件;④“非![]() 为真”是“
为真”是“![]() 且
且![]() 为假”的必要不充分条件.
为假”的必要不充分条件.
其中,正确的结论是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次跳绳活动中,某学校从高二年级抽取了100位同学一分钟内跳绳,由测量结果得到如图所示的频率分布直方图,落在区间[140,150),[150,160),[160,170]内的频率之比为4:2:1.
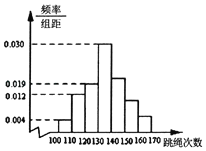
(1)求跳绳次数落在区间[150,160)内的频率;
(2)用分层抽样的方法在区间[130,160)内抽取6位同学,将该样本看成一个总体,从中任意抽取2位同学,求这2位同学跳绳次数都在区间[130,150)内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圈
分别是椭圈![]() 的左、右焦点,
的左、右焦点,![]() 是椭圆上第二象限内的一点且
是椭圆上第二象限内的一点且![]() 与
与![]() 轴垂直,直线
轴垂直,直线![]() 与椭圆的另一个交点为
与椭圆的另一个交点为![]() .
.
(1)若直线![]() 的斜率为
的斜率为![]() ,求椭圆的离心率;
,求椭圆的离心率;
(2)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,且
,且![]() 求
求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P到两定点M(﹣3,0),N(3,0)的距离满足|PM|=2|PN|.
(1)求证:点P的轨迹为圆;
(2)记(1)中轨迹为⊙C,过定点(0,1)的直线l与⊙C交于A,B两点,求△ABC面积的最大值,并求此时直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018、2019每高考数学全国Ⅰ卷中,第22题考查坐标系和参数方程,第23题考查不等式选讲.2018年髙考结束后,某校经统计发现:选择第22题的考生较多并且得分率也较高.为研究2019年选做题得分情况,该校高三质量检测的命题完全采用2019年高考选做题模式,在测试结束后,该校数学教师对全校高三学生的选做题得分进行抽样统计,得到两题得分的统计表如下(已知每名学生只选做—道题):
第22题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 50 | 50 | 75 | 125 | 200 |
文科人数 | 25 | 25 | 125 | 0 | 25 |
第23题的得分统计表
得分 | 0 | 3 | 5 | 8 | 10 |
理科人数 | 30 | 52 | 58 | 60 | 200 |
文科人数 | 5 | 10 | 10 | 5 | 70 |
(1)完成如下2×2列联表,并判断能否有99%的把握认为“选做题的选择”与“文、理科的科类”有关;
选做22题 | 选做23题 | 总计 | |
理科人数 | |||
文科人数 | |||
总计 |
(2)若以全体高三学生选题的平均得分作为决策依据,如果你是考生,根据上面统计数据,你会选做哪道题,并说明理由.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com