
【题目】已知函数![]() ,
,![]() 是实数.
是实数.
(1)若函数![]() 是定义在
是定义在![]() 上的奇函数,求
上的奇函数,求![]() 的值,并求方程
的值,并求方程![]() 的解;
的解;
(2)若![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() ,方程
,方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;
;
(2)![]() ;
;
(3)![]() 或
或![]() ;
;
【解析】
(1)可根据奇函数性质![]() ,也可根据特殊点
,也可根据特殊点![]() 求
求![]() ,再进行验证即可;令
,再进行验证即可;令![]() 结合一元二次方程的解法即可求解;
结合一元二次方程的解法即可求解;
(2)可采用分离常数法得![]() 对任意的
对任意的![]() 恒成立,令
恒成立,令![]() ,
,![]() ,令
,令![]() ,则
,则![]() ,结合二次函数性质即可求解;
,结合二次函数性质即可求解;
(3)![]() 时,
时,![]() ,
,![]() 化简得
化简得![]() ,采用构造函数法,令
,采用构造函数法,令![]() ,转化为方程
,转化为方程![]() 在
在![]() 上有解,再结合二次函数对称轴与增减性进一步求解即可
上有解,再结合二次函数对称轴与增减性进一步求解即可
(1)方法一:因为函数![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,
所以![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
整理得![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() .
.
方法二:因为函数![]() 是定义在
是定义在![]() 上的奇函数,所以
上的奇函数,所以![]() ,解得
,解得![]()
检验:当![]() 时,
时,![]() ,
,
此时,![]()
所以![]()
此时![]() .
.
因为![]() ,即
,即![]() ,整理得
,整理得![]()
解得![]() 或
或![]() (舍).
(舍).
所以![]() .
.
(2)因为![]() 对任意的
对任意的![]() 恒成立,
恒成立,
所以![]() ,即
,即![]() 对任意的
对任意的![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,
,
令![]() ,所以
,所以![]()
![]() 在
在![]() 上单调递增,
上单调递增,
所以![]()
所以![]() ,所以
,所以![]() .
.
(3)当![]() 时,
时,![]() ,因为
,因为![]() ,
,
所以![]() .
.
令![]() ,则
,则![]() ,
,
转化为方程![]() 在
在![]() 上有解.
上有解.
令![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 为增函数
为增函数
所以![]() ,得
,得![]() .
.
②当![]() 时,需
时,需![]() ,
,
即 ,解得
,解得![]() ,
,
所以![]() 或
或![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() ,集合
,集合![]() ,集合
,集合![]() .
.
(1)用列举法表示集合C;
(2)设集合C的含n个元素所有子集为![]() ,记有限集合M的所有元素和为
,记有限集合M的所有元素和为![]() ,求
,求![]()
![]() 的值;
的值;
(3)已知集合P、Q是集合C的两个不同子集,若P不是Q的子集,且Q不是P的子集,求所有不同的有序集合对![]() 的个数
的个数![]() ;
;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新能源汽车是我国汽车工业由大变强的一条必经之路!国家对其给予政策上的扶持,己成为我国的战略方针.近年来,我国新能源汽车制造蓬勃发展,某著名车企自主创新,研发了一款新能源汽车,经过大数据分析获得:在某种路面上,该品牌汽车的刹车距离![]() (米)与其车速
(米)与其车速![]() (千米/小时)满足下列关系:
(千米/小时)满足下列关系:![]() (
(![]() ,
,![]() 是常数).(行驶中的新能源汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离).如图是根据多次对该新能源汽车的实验数据绘制的刹车距离
是常数).(行驶中的新能源汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离).如图是根据多次对该新能源汽车的实验数据绘制的刹车距离![]() (米)与该车的车速
(米)与该车的车速![]() (千米/小时)的关系图.该新能源汽车销售公司为满足市场需求,国庆期间在甲、乙两地同时展销该品牌的新能源汽车,在甲地的销售利润(单位:万元)为
(千米/小时)的关系图.该新能源汽车销售公司为满足市场需求,国庆期间在甲、乙两地同时展销该品牌的新能源汽车,在甲地的销售利润(单位:万元)为![]() ,在乙地的销售利润(单位:万元)为
,在乙地的销售利润(单位:万元)为![]() ,其中
,其中![]() 为销售量(单位:辆).
为销售量(单位:辆).

(1)若该公司在两地共销售20辆该品牌的新能源汽车,则能获得的最大利润![]() 是多少?
是多少?
(2)如果要求刹车距离不超过25.2米,求该品牌新能源汽车行驶的最大速度.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂从今年一月起,若不改善生产环境,按生产现状,每月收入为80万元,同时将受到环保部门的处罚,第一个月罚4万元,以后每月增加2万元.如果从今年一月起投资500万元添加回收净化设备(改造设备时间不计),一方面可以改善环境,另一方面可以大大降低原料成本,据测算,添加回收净化设备并投产后的前4个月中的累计生产净收入g(n)是生产时间![]() 个月的二次函数
个月的二次函数![]() 是常数
是常数![]() ,且前3个月的累计生产净收入可达309万元,从第5个月开始,每个月的生产净收入都与第4个月相同,同时,该厂不但不受处罚,而且还将得到环保部门的一次性奖励120万元.
,且前3个月的累计生产净收入可达309万元,从第5个月开始,每个月的生产净收入都与第4个月相同,同时,该厂不但不受处罚,而且还将得到环保部门的一次性奖励120万元.
(1)求前6个月的累计生产净收入g(6)的值;
(2)问经过多少个月,投资开始见效,即投资改造后的纯收入多于不改造的纯收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,底面为正方形的四棱锥![]() 中,
中,![]() 平面
平面![]() ,
,![]() 为棱
为棱![]() 上一动点,
上一动点,![]() .
.

(1)当![]() 为
为![]() 中点时,求证:
中点时,求证:![]() 平面
平面![]() ;
;
(2)当![]() 平面
平面![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
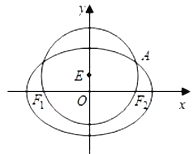
【题目】已知圆![]() :
: ![]() 经过椭圆
经过椭圆![]() :
: ![]() 的左右焦点
的左右焦点![]() ,且与椭圆
,且与椭圆![]() 在第一象限的交点为
在第一象限的交点为![]() ,且
,且![]() 三点共线,直线
三点共线,直线![]() 交椭圆
交椭圆![]() 于
于![]() ,
, ![]() 两点,且
两点,且![]() (
(![]() ).
).
(1)求椭圆![]() 的方程;
的方程;
(2)当三角形![]() 的面积取得最大值时,求直线
的面积取得最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
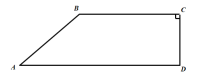
【题目】如图,某山地车训练中心有一直角梯形森林区域![]() ,其四条边均为道路,其中
,其四条边均为道路,其中![]() ,
,![]() ,
,![]() 千米,
千米,![]() 千米,
千米,![]() 千米.现有甲、乙两名特训队员进行野外对抗训练,要求同时从
千米.现有甲、乙两名特训队员进行野外对抗训练,要求同时从![]() 地出发匀速前往
地出发匀速前往![]() 地,其中甲的行驶路线是
地,其中甲的行驶路线是![]() ,速度为
,速度为![]() 千米/小时,乙的行驶路线是
千米/小时,乙的行驶路线是![]() ,速度为
,速度为![]() 千米/小时.
千米/小时.
(1)若甲、乙两名特训队员到达![]() 地的时间相差不超过
地的时间相差不超过![]() 分钟,求乙的速度
分钟,求乙的速度![]() 的取值范围;
的取值范围;
(2)已知甲、乙两名特训队员携带的无线通讯设备有效联系的最大距离是![]() 千米.若乙先于甲到达
千米.若乙先于甲到达![]() 地,且乙从
地,且乙从![]() 地到
地到![]() 地的整个过程中始终能用通讯设备对甲保持有效联系,求乙的速度
地的整个过程中始终能用通讯设备对甲保持有效联系,求乙的速度![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com