
ΓΨΧβΡΩΓΩ»γΆΦ,Ρ≥ΈέΥ°¥Πάμ≥ß“Σ‘Ύ“ΜΗωΨΊ–ΈΈέΥ°¥Πάμ≥Ί![]() ΒΡ≥ΊΒΉΥ°ΤΫΤΧ…ηΈέΥ°ΨΜΜ·ΙήΒάΘ®
ΒΡ≥ΊΒΉΥ°ΤΫΤΧ…ηΈέΥ°ΨΜΜ·ΙήΒάΘ®![]() Θ§
Θ§ ![]() «÷±Ϋ«ΕΞΒψΘ©ά¥¥ΠάμΈέΥ°Θ§ΙήΒά‘Ϋ≥ΛΘ§ΈέΥ°ΨΜΜ·–ßΙϊ‘ΫΚΟ.…ηΦΤ“Σ«σΙήΒάΒΡΫ”ΩΎ
«÷±Ϋ«ΕΞΒψΘ©ά¥¥ΠάμΈέΥ°Θ§ΙήΒά‘Ϋ≥ΛΘ§ΈέΥ°ΨΜΜ·–ßΙϊ‘ΫΚΟ.…ηΦΤ“Σ«σΙήΒάΒΡΫ”ΩΎ![]() «
«![]() ΒΡ÷–ΒψΘ§
ΒΡ÷–ΒψΘ§ ![]() Ζ÷±π¬δ‘ΎœΏΕΈ
Ζ÷±π¬δ‘ΎœΏΕΈ![]() …œ.“―÷Σ
…œ.“―÷Σ![]() ΟΉΘ§
ΟΉΘ§ ![]() ΟΉΘ§Φ«
ΟΉΘ§Φ«![]() .
.
Θ®1Θ© ‘ΫΪΈέΥ°ΨΜΜ·ΙήΒάΒΡΉή≥ΛΕ»![]() (Φ¥
(Φ¥![]() ΒΡ÷ή≥Λ)±μ ΨΈΣ
ΒΡ÷ή≥Λ)±μ ΨΈΣ![]() ΒΡΚ· ΐΘ§≤Δ«σ≥ωΕ®“ε”ρΘΜ
ΒΡΚ· ΐΘ§≤Δ«σ≥ωΕ®“ε”ρΘΜ
Θ®2Θ©Έ ![]() Β±»ΓΚΈ÷Β ±Θ§ΈέΥ°ΨΜΜ·–ßΙϊΉνΚΟΘΩ≤Δ«σ≥ω¥Υ ±ΙήΒάΒΡΉή≥ΛΕ».
Β±»ΓΚΈ÷Β ±Θ§ΈέΥ°ΨΜΜ·–ßΙϊΉνΚΟΘΩ≤Δ«σ≥ω¥Υ ±ΙήΒάΒΡΉή≥ΛΕ».
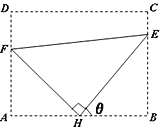
Θ®Χα ΨΘΚ ![]() .Θ©
.Θ©
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() Θ§Ε®“ε”ρΈΣ
Θ§Ε®“ε”ρΈΣ![]() .Θ®2Θ©Β±
.Θ®2Θ©Β±![]() Μρ
Μρ![]() ±ΥυΤΧ…ηΒΡΙήΒάΉνΕΧΘ§ΈΣ
±ΥυΤΧ…ηΒΡΙήΒάΉνΕΧΘ§ΈΣ![]() ΟΉ.
ΟΉ.
ΓΨΫβΈωΓΩ ‘ΧβΖ÷ΈωΘΚΘ®1Θ©»γΆΦΘ§“ρΈΣ![]() ΕΦ «÷±Ϋ«»ΐΫ«–ΈΘ§Ι Ω…“‘ΒΟΒΫ
ΕΦ «÷±Ϋ«»ΐΫ«–ΈΘ§Ι Ω…“‘ΒΟΒΫ![]() Θ§“≤ΨΆ «
Θ§“≤ΨΆ «![]() Θ§Τδ÷–
Θ§Τδ÷–![]() .Θ®2Θ©
.Θ®2Θ©![]() Ω…±δ–ΈΈΣ
Ω…±δ–ΈΈΣ![]() Θ§Νν
Θ§Νν![]() ΚσΘ§‘ρ”–
ΚσΘ§‘ρ”–![]() Θ§Τδ÷–
Θ§Τδ÷–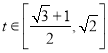 Θ§Ι
Θ§Ι ![]() »ΓΒΡΉν¥σ÷Β
»ΓΒΡΉν¥σ÷Β![]() ΟΉ.
ΟΉ.
ΫβΈωΘΚΘ®1Θ©![]() .
.
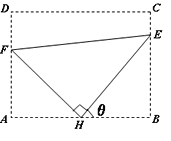
”…”Ύ![]() Θ§
Θ§ ![]() Θ§Υυ“‘
Θ§Υυ“‘![]() Θ§Ι
Θ§Ι ![]() .ΙήΒάΒΡΉή≥ΛΕ»
.ΙήΒάΒΡΉή≥ΛΕ»![]() Θ§Ε®“ε”ρΈΣ
Θ§Ε®“ε”ρΈΣ![]() .
.
(2) ![]() . …η
. …η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§Υυ“‘
Θ§Υυ“‘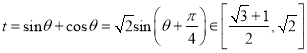 . “ρΈΣ
. “ρΈΣ![]() ‘Ύ
‘Ύ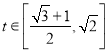 ΡΎΒΞΒςΒίΦθΘ§”Ύ «Β±
ΡΎΒΞΒςΒίΦθΘ§”Ύ «Β±![]() ±Θ§
±Θ§ ![]() »ΓΒΡΉν¥σ÷Β
»ΓΒΡΉν¥σ÷Β![]() ΟΉ. Θ®¥Υ ±
ΟΉ. Θ®¥Υ ±![]() Μρ
Μρ![]() Θ©.
Θ©.
¥πΘΚΒ±![]() Μρ
Μρ![]() ±ΥυΤΧ…ηΒΡΙήΒάΉνΕΧΘ§ΈΣ
±ΥυΤΧ…ηΒΡΙήΒάΉνΕΧΘ§ΈΣ![]() ΟΉ.
ΟΉ.


 ±Η’Ϋ÷–ΩΦΚ°ΦΌœΒΝ–¥πΑΗ
±Η’Ϋ÷–ΩΦΚ°ΦΌœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηSΘΫ{x|xΘΫmΘΪn![]() Θ§mΓΔnΓ Z}Θ°
Θ§mΓΔnΓ Z}Θ°
(1)»τaΓ ZΘ§‘ρa «Ζώ «Φ·ΚœS÷–ΒΡ‘ΣΥΊΘΩ
(2)Ε‘S÷–ΒΡ»Έ“βΝΫΗωx1ΓΔx2Θ§‘ρx1ΘΪx2ΓΔx1ΓΛx2 «Ζώ τ”ΎSΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ,‘ΎΥΡάβΉΕ![]() ÷–,ΒΉΟφ
÷–,ΒΉΟφ![]() ΈΣΤΫ––ΥΡ±Ώ–Έ,
ΈΣΤΫ––ΥΡ±Ώ–Έ, ![]() ΈΣ≤ύάβ
ΈΣ≤ύάβ![]() ΒΡ÷–Βψ.
ΒΡ÷–Βψ.

Θ®ΔώΘ©«σ÷Λ: ![]() ΓΈΤΫΟφ
ΓΈΤΫΟφ![]()
Θ®ΔρΘ©»τ![]() ,
,![]() ,
,
«σ÷Λ:ΤΫΟφ![]()
![]() ΤΫΟφ
ΤΫΟφ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΒψAΒΡΉχ±ξΈΣΘ®4Θ§1Θ©Θ§ΒψBΘ®©¹7Θ§©¹2Θ©ΙΊ”Ύ÷±œΏy=xΒΡΕ‘≥ΤΒψΈΣCΘ°
Θ®ΔώΘ©«σ“‘AΓΔCΈΣ÷±ΨΕΒΡ‘≤EΒΡΖΫ≥ΧΘΜ
Θ®ΔρΘ©…ηΨ≠ΙΐΒψAΒΡ÷±œΏl”κ‘≤EΒΡΝμ“ΜΗωΫΜΒψΈΣDΘ§|AD|=8Θ§«σ÷±œΏlΒΡΖΫ≥ΧΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΥυ ΨΘ§‘ΎΥΡάβΉΕA©¹BCDE÷–Θ§ABΓΆΤΫΟφBCDEΘ§ΥΡ±Ώ–ΈBCDEΈΣΨΊ–ΈΘ§FΈΣACΒΡ÷–ΒψΘ§AB=BC=2Θ§BE= ![]() Θ°
Θ°
Θ®ΔώΘ©÷ΛΟςΘΚEFΓΆBDΘΜ
Θ®ΔρΘ©‘ΎœΏΕΈAE…œ «Ζώ¥φ‘Ύ“ΜΒψGΘ§ ΙΒΟΕΰΟφΫ«D©¹BG©¹EΒΡ¥σ–ΓΈΣ ![]() ΘΩ»τ¥φ‘ΎΘ§«σ
ΘΩ»τ¥φ‘ΎΘ§«σ ![]() ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
ΒΡ÷ΒΘΜ»τ≤Μ¥φ‘ΎΘ§ΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ…ηΙΐ≈ΉΈοœΏy2=4xΒΡΫΙΒψFΒΡ÷±œΏlΫΜ≈ΉΈοœΏ”ΎΒψAΘ§BΘ§»τ“‘ABΈΣ÷±ΨΕΒΡ‘≤ΙΐΒψPΘ®©¹1Θ§2Θ©Θ§«“”κx÷αΫΜ”ΎMΘ®mΘ§0Θ©Θ§NΘ®nΘ§0Θ©ΝΫΒψΘ§‘ρmn=Θ® Θ©
A.3
B.2
C.©¹3
D.©¹2
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΚ· ΐ![]() Θ§
Θ§ ![]() ΈΣ≥Θ ΐΘ°
ΈΣ≥Θ ΐΘ°
Θ®![]() Θ©»τ
Θ©»τ![]() Θ§«σ
Θ§«σ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
Θ®![]() Θ©»τΕ‘»Έ“βΒΡ
Θ©»τΕ‘»Έ“βΒΡ![]() ΕΦ”–≤ΜΒ» Ϋ
ΕΦ”–≤ΜΒ» Ϋ![]() ≥…ΝΔΘ§«σ
≥…ΝΔΘ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
Θ®![]() Θ©‘ΎΘ®
Θ©‘ΎΘ®![]() Θ©ΒΡΧθΦΰœ¬Θ§»τΚ· ΐ
Θ©ΒΡΧθΦΰœ¬Θ§»τΚ· ΐ![]() ΒΡΆΦœώ”κ
ΒΡΆΦœώ”κ![]() ÷α«Γ”–»ΐΗωœύ“λΒΡΙΪΙ≤ΒψΘ§«σ Β ΐ
÷α«Γ”–»ΐΗωœύ“λΒΡΙΪΙ≤ΒψΘ§«σ Β ΐ![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ{an} «ΙΪ≤ν≤ΜΈΣΝψΒΡΒ»≤ν ΐΝ–Θ§a1=1Θ§«“a1 Θ§ a3 Θ§ a9≥…Β»±» ΐΝ–Θ°
Θ®1Θ©«σ ΐΝ–{an}ΒΡΆ®œνΘΜ
Θ®2Θ©…η ΐΝ–{an}ΒΡ«ΑnœνΚΆΈΣSn Θ§ Νν ![]() Θ§«σ ΐΝ–{bn}ΒΡ«ΑnœνΚΆTn Θ°
Θ§«σ ΐΝ–{bn}ΒΡ«ΑnœνΚΆTn Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΡ≥≥« –…œΡξΕ»ΒγΦέΈΣ0.80‘Σ/«ßΆΏ ±Θ§Ρξ”ΟΒγΝΩΈΣ![]() «ßΆΏ ±.±ΨΡξΕ»ΦΤΜ°ΫΪΒγΦέΫΒΒΫ0.55‘Σ/«ßΆΏ ±ΓΪ0.7‘Σ/«ßΆΏ ±÷°ΦδΘ§ΕχΨ”Οώ”ΟΜßΤΎΆϊΒγΦέΈΣ0.40‘Σ/«ßΆΏ ±Θ®ΗΟ –ΒγΝΠ≥…±ΨΦέΈΣ0.30‘Σ/«ßΆΏ ±)Θ§Ψ≠≤βΥψΘ§œ¬ΒςΒγΦέΚσΘ§ΗΟ≥« ––¬‘ω”ΟΒγΝΩ”κ ΒΦ ΒγΦέΚΆ”ΟΜßΤΎΆϊΒγΦέ÷°≤ν≥…Ζ¥±»Θ§±»άΐœΒ ΐΈΣ
«ßΆΏ ±.±ΨΡξΕ»ΦΤΜ°ΫΪΒγΦέΫΒΒΫ0.55‘Σ/«ßΆΏ ±ΓΪ0.7‘Σ/«ßΆΏ ±÷°ΦδΘ§ΕχΨ”Οώ”ΟΜßΤΎΆϊΒγΦέΈΣ0.40‘Σ/«ßΆΏ ±Θ®ΗΟ –ΒγΝΠ≥…±ΨΦέΈΣ0.30‘Σ/«ßΆΏ ±)Θ§Ψ≠≤βΥψΘ§œ¬ΒςΒγΦέΚσΘ§ΗΟ≥« ––¬‘ω”ΟΒγΝΩ”κ ΒΦ ΒγΦέΚΆ”ΟΜßΤΎΆϊΒγΦέ÷°≤ν≥…Ζ¥±»Θ§±»άΐœΒ ΐΈΣ![]() . ‘Έ Β±ΒΊΒγΦέΉνΒΆΈΣΕύ…Ό‘Σ/«ßΆΏ ±Θ§Ω…±Θ÷ΛΒγΝΠ≤ΩΟ≈ΒΡ ’“φ±»…œΡξΕ»÷Ν…Ό‘ωΦ”20%.
. ‘Έ Β±ΒΊΒγΦέΉνΒΆΈΣΕύ…Ό‘Σ/«ßΆΏ ±Θ§Ω…±Θ÷ΛΒγΝΠ≤ΩΟ≈ΒΡ ’“φ±»…œΡξΕ»÷Ν…Ό‘ωΦ”20%.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com