[题目]设双曲线的左.右焦点分别为F1.F2.过F1的直线l交双曲线左支于A.B两点.则|BF2|+|AF2|的最小值为( )A. B. 11C. 12 D. 16 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】设双曲线的左，右焦点分别为F1，F2，过F1的直线l交双曲线左支于A，B两点，则|BF2|＋|AF2|的最小值为(　　)

A. B. 11

C. 12 D. 16

【答案】B

【解析】由-=1知a2=4,b2=3,

∴c2=7,c=,∴F1(-,0),F2(,0),

又点A、B在双曲线左支上,

∴|AF2|-|AF1|=4,|BF2|-|BF1|=4,

∴|AF2|=4+|AF1|,|BF2|=4+|BF1|,

∴|AF2|+|BF2|=8+|AF1|+|BF1|.

要求|AF2|+|BF2|的最小值,只要求|AF1|+|BF1|的最小值,而|AF1|+|BF1|最小为2×=3.

∴(|AF2|+|BF2|)min=8+3=11.故选B.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】如图，在四棱锥S﹣ABCD中，底面ABCD是边长为2的正方形，SA＝SB＝SC＝SD，点E，M，N分别是BC，CD，SC的中点，点P是MN上的一点．

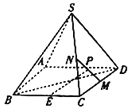
（1）证明：EP∥平面SBD；

（2）求四棱锥S﹣ABCD的表面积．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】（1）已知，求的最大值；

（2）已知，求的最小值；

（3）已知，求的最大值；

（4）求函数的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某商场举行促销活动，有两个摸奖箱，箱内有一个“”号球、两个“”号球、三个“”号球、四个无号球，箱内有五个“”号球、五个“”号球，每次摸奖后放回，消费额满元有一次箱内摸奖机会，消费额满元有一次箱内摸奖机会，摸得有数字的球则中奖，“”号球奖元、“”号球奖元、“”号球奖元，摸得无号球则没有奖金.

（Ⅰ）经统计，消费额服从正态分布，某天有为顾客，请估计消费额（单位：元）在区间内并中奖的人数；

（Ⅱ）某三位顾客各有一次箱内摸奖机会，求其中中奖人数的分布列；

（Ⅲ）某顾客消费额为元，有两种摸奖方法，方法一：三次箱内摸奖机会；方法二：一次箱内摸奖机会，请问：这位顾客选哪一种方法所得奖金的期望值较大.

附：若，则

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数 .

（Ⅰ）若在区间上有极值，求实数的取值范围；

（Ⅱ）若有唯一的零点，试求的值.（注：为取整函数，表示不超过的最大整数，如；以下数据供参考：）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】

两县城A和B相聚20km，现计划在两县城外以AB为直径的半圆弧上选择一点C建造垃圾处理厂，其对城市的影响度与所选地点到城市的的距离有关，对城A和城B的总影响度为城A与城B的影响度之和，记C点到城A的距离为x km，建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明：垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比，比例系数为4；对城B的影响度与所选地点到城B的距离的平方成反比，比例系数为k ,当垃圾处理厂建在的中点时，对称A和城B的总影响度为0.0065.（1）将y表示成x的函数；（11）讨论（1）中函数的单调性，并判断弧上是否存在一点，使建在此处的垃圾处理厂对城A和城B的总影响度最小？若存在，求出该点到城A的距离，若不存在，说明理由。