
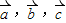 为三个向量,则
为三个向量,则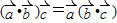 ”
”

 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:高中数学 来源: 题型:
| a+b |
| 2 |
| a+b |
| 2 |
| a+b |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| b |
| c |
| a |
| b |
| c |
| a |
| b |
| c |
| π |
| 4 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•徐汇区三模)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:
(2011•徐汇区三模)定义:由椭圆的两个焦点和短轴的一个顶点组成的三角形称为该椭圆的“特征三角形”.如果两个椭圆的“特征三角形”是相似的,则称这两个椭圆是“相似椭圆”,并将三角形的相似比称为椭圆的相似比.已知椭圆C1:| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 组别 | A | B | C | D | E |
| 人数 | 100 | 50 | 150 | 50 | 150 |
| 组别 | A | B | C | D | E |
| 人数 | 100 | 50 | 150 | 50 | 150 |
| 抽取人数 | 6 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川省高三10月月考理科数学试卷(解析版) 题型:选择题
甲乙二人玩猜数字游戏,先由甲任想一数字,记为a,再由乙猜甲刚才想的数字,把乙猜出的数字记为b,且a,b∈{1,2,3},若|a-b| ≤ 1,则称甲乙“心有灵犀”,现任意找两个人玩这个游戏,则他们“心有灵犀”的概率为
A.  B.
B.
 C.
C.
 D.
D.
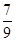
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com