
【题目】某省级示范高中高三年级对各科考试的评价指标中,有“难度系数“和“区分度“两个指标中,难度系数![]() ,区分度
,区分度![]() .
.
(1)某次数学考试(满分为150分),随机从实验班和普通班各抽取三人,实验班三人的成绩分别为147,142,137;普通班三人的成绩分别为97,102,113.通过样本估计本次考试的区分度(精确0.01).
(2)如表表格是该校高三年级6次数学考试的统计数据:
难度系数x | 0.64 | 0.71 | 0.74 | 0.76 | 0.77 | 0.82 |
区分度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
①计算相关系数r,|r|<0.75时,认为相关性弱;|r|≥0.75时,认为相关性强.通过计算说明,能否利用线性回归模型描述y与x的关系(精确到0.01).
②ti=|xi﹣0.74|(i=1,2,…,6),求出y关于t的线性回归方程,并预测x=0.75时y的值(精确到0.01).
附注:参考数据: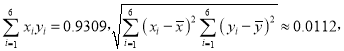
![]()
![]()
参考公式:相关系数 r,回归直线
r,回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
【答案】(1)0.25;(2)①理由见解析,不能利用线性回归模型描述y与x的关系; ② 回归直线方程![]() ,预测值为0.24
,预测值为0.24
【解析】
(1)先求出平均成绩,即可求出区分度;
(2)①由题意计算,求出相关系数,即可判断两变量相关性强弱;
②计算回归系数,写出线性回归方程,利用方程计算t=10时的值.
(1)实验班三人成绩的平均值为![]() ,
,
普通班三人成绩的平均值为![]() ,
,
故估计本次考试的区分度为![]() 0.25,
0.25,
(2)①由题中的表格可知![]() (0.64+0.71+0.74+0.76+0.77+0.82)=0.74,
(0.64+0.71+0.74+0.76+0.77+0.82)=0.74,
![]() (0.18+0.23+0.24+0.24+0.22+0.15)=0.21,
(0.18+0.23+0.24+0.24+0.22+0.15)=0.21,
故r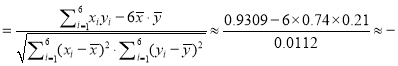 0.13.
0.13.
因为|r|<0.75,所以相关性弱,故不能利用线性回归模型描述y与x的关系;
②y与t的值如下表
t | 0.10 | 0.03 | 0 | 0.02 | 0.03 | 0.08 |
区别度y | 0.18 | 0.23 | 0.24 | 0.24 | 0.22 | 0.15 |
因为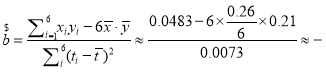 0.86,
0.86,
所以a![]() 0.21+0.86
0.21+0.86![]() 0.25,
0.25,
所以所求回归直线方程y=﹣0.86t+0.25,
当x=0.75时,此时t=0.01,则y≈0.24


 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A.若“![]() ”为真命题,则“
”为真命题,则“![]() ”为真命题
”为真命题
B.命题“![]() ”的否定是“
”的否定是“![]() ”
”
C.命题“若![]() ,则
,则![]() ”的逆否命题为真命题
”的逆否命题为真命题
D.“![]() ”是“
”是“![]() ”的必要不充分条件
”的必要不充分条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2013年华人数学家张益唐证明了孪生素数猜想的一个弱化形式.孪生素数猜想是希尔伯特在二十世纪初提出的23个数学问题之一.可以这样描述:存在无穷多个素数![]() ,使得
,使得![]() 是素数,称素数对
是素数,称素数对![]() 为孪生素数.在不超过15的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( ).
为孪生素数.在不超过15的素数中,随机选取两个不同的数,其中能够组成孪生素数的概率是( ).
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
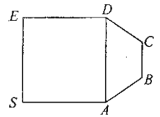
【题目】某产品的包装纸可类比如图所示的平面图形,其可看作是由正方形![]() 和等腰梯形
和等腰梯形![]() 拼成,已知
拼成,已知![]() ,
,![]() ,在包装的过程中,沿着
,在包装的过程中,沿着![]() 将正方形
将正方形![]() 折起,直至
折起,直至![]() ,得到多面体
,得到多面体![]() ,
,![]() 分别为
分别为![]() 中点.
中点.
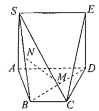
(1)证明:![]() 平面
平面![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题正确的个数为( )
①“![]() 都有
都有![]() ”的否定是“
”的否定是“![]() 使得
使得![]() ”;
”;
②“![]() ”是“
”是“![]() ”成立的充分条件;
”成立的充分条件;
③命题“若![]() ,则方程
,则方程![]() 有实数根”的否命题;
有实数根”的否命题;
④幂函数的图像可以出现在第四象限.
A.0B.1C.2D.3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com