
【题目】设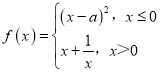 .
.
(1)当![]() 时,f(x)的最小值是_____;
时,f(x)的最小值是_____;
(2)若f(0)是f(x)的最小值,则a的取值范围是_____.
【答案】![]() [0,
[0,![]() ]
]
【解析】
(1)先求出分段函数的每一段的最小值,再求函数的最小值;(2)对![]() 分两种情况讨论,若a<0,不满足条件.若a≥0,f(0)=a2≤2,即0≤a
分两种情况讨论,若a<0,不满足条件.若a≥0,f(0)=a2≤2,即0≤a![]() ,即得解.
,即得解.
(1)当![]() 时,当x≤0时,f(x)=(x
时,当x≤0时,f(x)=(x![]() )2≥(
)2≥(![]() )2
)2![]() ,
,
当x>0时,f(x)=x![]() 2
2![]() 2,当且仅当x=1时取等号,
2,当且仅当x=1时取等号,
则函数的最小值为![]() ,
,
(2)由(1)知,当x>0时,函数f(x)≥2,此时的最小值为2,
若a<0,则当x=a时,函数f(x)的最小值为f(a)=0,此时f(0)不是最小值,不满足条件.
若a≥0,则当x≤0时,函数f(x)=(x﹣a)2为减函数,
则当x≤0时,函数f(x)的最小值为f(0)=a2,
要使f(0)是f(x)的最小值,则f(0)=a2≤2,即0≤a![]() ,
,
即实数a的取值范围是[0,![]() ]
]


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度![]() (图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).
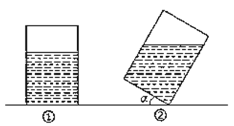
(1)要使倾斜后容器内的溶液不会溢出,角![]() 的最大值是多少?
的最大值是多少?
(2)现需要倒出不少于![]() 的溶液,当
的溶液,当![]() 时,能实现要求吗?请说明理由.
时,能实现要求吗?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,![]() 平面PCD,
平面PCD,![]() ,
,![]() ,
,![]() ,E为AD的中点,AC与BE相交于点O.
,E为AD的中点,AC与BE相交于点O.

(1)证明:![]() 平面ABCD.
平面ABCD.
(2)求直线BC与平面PBD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的首项
的首项![]() ,对任意的
,对任意的![]() ,都有
,都有![]() ,数列
,数列![]() 是公比不为
是公比不为![]() 的等比数列.
的等比数列.
(1)求实数![]() 的值;
的值;
(2)设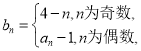 数列
数列![]() 的前
的前![]() 项和为
项和为![]() ,求所有正整数
,求所有正整数![]() 的值,使得
的值,使得![]() 恰好为数列
恰好为数列![]() 中的项.
中的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数,且
为常数,且![]() .
.
(1)若![]() 是奇函数,求
是奇函数,求![]() 的取值集合
的取值集合![]() ;
;
(2)当![]() 时,设
时,设![]() 的反函数
的反函数![]() ,且
,且![]() 的图象与
的图象与![]() 的图象关于
的图象关于![]() 对称,求
对称,求![]() 的取值集合
的取值集合![]() ;
;
(3)对于问题(1)(2)中的![]() 、
、![]() ,当
,当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:直线关于圆的圆心距单位![]() 圆心到直线的距离与圆的半径之比.
圆心到直线的距离与圆的半径之比.
(1)设圆![]() ,求过点
,求过点![]() 的直线关于圆
的直线关于圆![]() 的圆心距单位
的圆心距单位![]() 的直线方程.
的直线方程.
(2)若圆![]() 与
与![]() 轴相切于点
轴相切于点![]() ,且直线
,且直线![]() 关于圆
关于圆![]() 的圆心距单位
的圆心距单位![]() ,求此圆
,求此圆![]() 的方程.
的方程.
(3)是否存在点![]() ,使过点
,使过点![]() 的任意两条互相垂直的直线分别关于相应两圆
的任意两条互相垂直的直线分别关于相应两圆![]() 与
与![]() 的圆心距单位始终相等?若存在,求出相应的
的圆心距单位始终相等?若存在,求出相应的![]() 点坐标;若不存在,请说明理由.
点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com