
【题目】(本小题满分12分)已知圆C过点P(1,1),且与圆M:![]() 关于直线
关于直线![]() 对称.
对称.
(1)求圆C的方程:
(2)设Q为圆C上的一个动点,求![]() 最小值;
最小值;
(3)过点P作两条相异直线分别与圆C交与A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP与直线AB是否平行?请说明理由.
【答案】(1)![]() ;(2)-4;(3)平行.
;(2)-4;(3)平行.
【解析】
试题(1)由题意圆心![]() 与圆心
与圆心![]() 关于直线
关于直线![]() 对称;(2)设
对称;(2)设![]() ,由(1)有
,由(1)有![]() ,
,![]() ,可设
,可设![]() ,代入可求得
,代入可求得![]() 的最小值;(3)本题证明用解析法,由于直线PA和直线PB的倾斜角互补,设
的最小值;(3)本题证明用解析法,由于直线PA和直线PB的倾斜角互补,设![]() 方程为
方程为![]() ,则
,则![]() 方程为
方程为![]() ,把它们代入圆
,把它们代入圆![]() 的方程求得
的方程求得![]() 的坐标,计算得
的坐标,计算得![]() ,即
,即![]() .
.
试题解析:(1)设圆心C(a,b),则 解得 a=0 b=0
解得 a=0 b=0
所以圆C的方程为![]() , 将点P的坐标代人得
, 将点P的坐标代人得![]() , 所以圆C的方程为
, 所以圆C的方程为![]() .
.
(2)设Q(x,y) ,则![]()
所以![]()
所以![]() 的最小值为 -4 (可由线性规划或三角代换求得)
的最小值为 -4 (可由线性规划或三角代换求得)
(3)由题意可知,直线PA和直线PB的斜率存在且互为相反数
故 可设PA:![]() PB:
PB:![]()
由 得
得![]()
因为点P的横坐标是 x=1,一定是方程的解 故可得![]()
同理![]()
所以 ![]()
所以直线OP与直线AB一定平行.


科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四们同学一起去向老师询问数学学业水平考试成绩等级. 老师说:“你们四人中有2人![]() 等,1人
等,1人![]() 等,1人
等,1人![]() 等,我现在给甲看乙、丙的成绩等级,给乙看丙的成绩等级,给丙看丁的成绩等级”.看后甲对大家说:“我知道我的成绩等级了”.根据以上信息,则( )
等,我现在给甲看乙、丙的成绩等级,给乙看丙的成绩等级,给丙看丁的成绩等级”.看后甲对大家说:“我知道我的成绩等级了”.根据以上信息,则( )
A. 甲、乙的成绩等级相同 B. 丁可以知道四人的成绩等级
C. 乙、丙的成绩等级相同 D. 乙可以知道四人的成绩等级
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为增强学生体质,学校组织体育社团,某宿舍有4人积极报名参加篮球和足球社团,每人只能从两个社团中选择其中一个社团,大家约定:每个人通过掷一枚质地均匀的骰子决定自己参加哪个社团,掷出点数为5或6的人参加篮球社团,掷出点数小于5的人参加足球社团.
(Ⅰ)求这4人中恰有1人参加篮球社团的概率;
(Ⅱ)用![]() 分别表示这4人中参加篮球社团和足球社团的人数,记随机变量
分别表示这4人中参加篮球社团和足球社团的人数,记随机变量![]() 为
为![]() 和
和![]() 的乘积,求随机变量
的乘积,求随机变量![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大指出中国的电动汽车革命早已展开,通过以新能源汽车替代汽/柴油车,中国正在大力实施一项将重塑全球汽车行业的计划.![]() 年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本
年某企业计划引进新能源汽车生产设备,通过市场分析,全年需投入固定成本![]() 万元,每生产
万元,每生产![]() (百辆),需另投入成本
(百辆),需另投入成本![]() 万元,且
万元,且 .由市场调研知,每辆车售价
.由市场调研知,每辆车售价![]() 万元,且全年内生产的车辆当年能全部销售完.
万元,且全年内生产的车辆当年能全部销售完.
(1)求出2018年的利润![]() (万元)关于年产量
(万元)关于年产量![]() (百辆)的函数关系式;(利润=销售额-成本)
(百辆)的函数关系式;(利润=销售额-成本)
(2)2018年产量为多少百辆时,企业所获利润最大?并求出最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 或
或![]() ,
,![]() ,
,![]() .
.
![]() 从以下两个命题中任选一个进行证明:
从以下两个命题中任选一个进行证明:
![]() 当
当![]() 时函数
时函数![]() 恰有一个零点;
恰有一个零点;
![]() 当
当![]() 时函数
时函数![]() 恰有一个零点;
恰有一个零点;
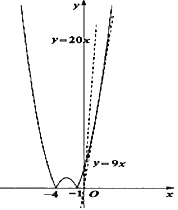
![]() 如图所示当
如图所示当![]() 时
时![]() 如
如![]() ,
,![]() 与
与![]() 的图象“好像”只有一个交点,但实际上这两个函数有两个交点,请证明:当
的图象“好像”只有一个交点,但实际上这两个函数有两个交点,请证明:当![]() 时,
时,![]() 与
与![]() 两个交点.
两个交点.
![]() 若方程
若方程![]() 恰有4个实数根,请结合
恰有4个实数根,请结合![]() 的研究,指出实数k的取值范围
的研究,指出实数k的取值范围![]() 不用证明
不用证明![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com