
°æƒø°ø»’’’“ª÷–Œ™¡À¬‰ µ°∞—Ùπ‚‘À∂Ø“ª–° ±°±ªÓ∂Ø£¨º∆ªÆ‘⁄“ªøÈ÷±Ω«»˝Ω«–ŒABCµƒø’µÿ…œ–ÞΩ®“ª∏ˆ’ºµÿ√ʪ˝Œ™Sµƒæÿ–ŒAMPNΩ°…Ì≥°µÿ£Æ»ÁÕº£¨µ„M‘⁄AC…œ£¨µ„N‘⁄AB…œ£¨«“Pµ„‘⁄–±±þBC…œ£¨“—÷™°œACB=60°„«“|AC|=30√◊£¨|AM|=x√◊£¨x° [10£¨20]£Æ
£®1£© ‘”√x±Ì æS£¨≤¢«ÛSµƒ»°÷µ∑∂Œß£ª
£®2£©»Ù‘⁄æÿ–ŒAMPN“‘Õ‚£®“ı”∞≤ø∑÷£©∆Ã…œ≤ð∆∫£Æ“—÷™£∫æÿ–ŒAMPNΩ°…Ì≥°µÿ√ø∆Ω∑Ω√◊µƒ‘Ϻ€Œ™![]() £¨≤ð∆∫µƒ√ø∆Ω∑Ω√◊µƒ‘Ϻ€Œ™
£¨≤ð∆∫µƒ√ø∆Ω∑Ω√◊µƒ‘Ϻ€Œ™![]() £®kŒ™’˝≥£ ˝£©£Æ…Ë◊БϺ€Tπÿ”⁄Sµƒ∫Ø ˝Œ™T=f£®S£©£¨ ‘Œ £∫»Á∫Œ—°»°|AM|µƒ≥§£¨≤≈ƒÐ π◊БϺ€T◊ÓµÕ£Æ
£®kŒ™’˝≥£ ˝£©£Æ…Ë◊БϺ€Tπÿ”⁄Sµƒ∫Ø ˝Œ™T=f£®S£©£¨ ‘Œ £∫»Á∫Œ—°»°|AM|µƒ≥§£¨≤≈ƒÐ π◊БϺ€T◊ÓµÕ£Æ

°æ¥∞∏°ø£®1£©![]() £®2£©12√◊ªÚ18√◊
£®2£©12√◊ªÚ18√◊
°æΩ‚Œˆ°ø
‘£®1£©∏˘æð“‚£¨∑÷Œˆø…µ√£¨”˚«ÛΩ°…Ì≥°µÿ’ºµÿ√ʪ˝£¨÷ª–ΫÛ≥ˆÕº÷–æÿ–Œµƒ√ʪ˝º¥ø…£¨‘ŸΩ·∫œæÿ–Œµƒ√ʪ˝º∆À„π´ Ω«Û≥ˆÀ¸√«µƒ√ʪ˝º¥µ√£¨◊Ó∫Û‘Ÿ∏˘æð∂˛¥Œ∫Ø ˝µƒ–‘÷ µ√≥ˆ∆‰∑∂Œß£ª
£®2£©∂‘”⁄£®1£©À˘¡–≤ªµ» Ω£¨øº¬«µΩ∆‰÷–¡ΩœÓ÷ƪ˝Œ™∂®÷µ£¨ø…¿˚”√ª˘±æ≤ªµ» Ω«ÛÀ¸µƒ◊Ó¥Û÷µ£¨¥”∂¯Ω‚戌 £Æ
Ω‚£∫£®1£©‘⁄Rt°˜PMC÷–£¨œ‘»ª|MC|=30©Åx£¨°œPCM=60°„
°ý|PM|=|MC|tan°œPCM=![]() £®30©Åx£©£¨°≠2∑÷
£®30©Åx£©£¨°≠2∑÷
æÿ–ŒAMPNµƒ√ʪ˝S=|PM||MC|=![]() x£®30©Åx£©£¨x° [10£¨20]°≠4∑÷
x£®30©Åx£©£¨x° [10£¨20]°≠4∑÷
”⁄ «200![]() °ÐS°Ð225
°ÐS°Ð225![]() Œ™À˘«Û£Æ°≠6∑÷
Œ™À˘«Û£Æ°≠6∑÷
£®2£©æÿ–ŒAMPNΩ°…Ì≥°µÿ‘Ϻ€T1=37k![]() °≠7∑÷
°≠7∑÷
”÷°˜ABCµƒ√ʪ˝Œ™450![]() £¨º¥≤ð∆∫‘Ϻ€T2=
£¨º¥≤ð∆∫‘Ϻ€T2=![]() S£©°≠8∑÷
S£©°≠8∑÷
”…◊БϺ€T=T1+T2£¨°ýT=25k£®![]() +
+![]() £©£¨200
£©£¨200![]() °ÐS°Ð225
°ÐS°Ð225![]() £Æ°≠10∑÷
£Æ°≠10∑÷
°ýT=25k£®![]() +
+![]() £©£¨200
£©£¨200![]() °ÐS°Ð225
°ÐS°Ð225![]()
°þ![]() +
+![]() °ð12
°ð12![]() £¨°≠11∑÷
£¨°≠11∑÷
µ±«“Ωˆµ±![]() =
=![]() º¥S=216
º¥S=216![]() ±µ»∫≈≥…¡¢£¨°≠12∑÷
±µ»∫≈≥…¡¢£¨°≠12∑÷
¥À ±![]() x£®30©Åx£©=216
x£®30©Åx£©=216![]() £¨Ω‚µ√x=12ªÚx=18£¨
£¨Ω‚µ√x=12ªÚx=18£¨
À˘“‘—°»°|AM|µƒ≥§Œ™12√◊ªÚ18√◊ ±◊БϺ€T◊ӵգư≠14∑÷£Æ


 ‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
‘ƒ∂¡øÏ≥µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™À´«˙œþ![]() µƒ¡Ω∏ˆΩπµ„Œ™
µƒ¡Ω∏ˆΩπµ„Œ™![]() °¢
°¢![]() £¨PŒ™∏√À´«˙œþ…œ“ªµ„£¨¬˙◊„
£¨PŒ™∏√À´«˙œþ…œ“ªµ„£¨¬˙◊„![]() £¨PµΩ◊¯±Í‘≠µ„Oµƒæý¿ÎŒ™d£¨«“
£¨PµΩ◊¯±Í‘≠µ„Oµƒæý¿ÎŒ™d£¨«“![]() £¨‘Ú
£¨‘Ú![]() ________.
________.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø◊‘»ª◊¥Ã¨œ¬µƒ”„¿ý «“ª÷÷ø…‘Ÿ…˙◊ ‘¥£¨Œ™¡À≥÷–¯¿˚”√’‚“ª◊ ‘¥£¨–Ë¥”∫Íπ€…œøº≤Ï∆‰‘Ÿ…˙ƒÐ¡¶º∞≤∂¿Ã«ø∂»∂‘”„»∫◊Сøµƒ”∞œÏ.”√![]() ±Ì æƒ≥”„»∫‘⁄µ⁄
±Ì æƒ≥”„»∫‘⁄µ⁄![]() ƒÍƒÍ≥ıµƒ◊Сø«“
ƒÍƒÍ≥ıµƒ◊Сø«“![]() .≤ªøº¬«∆‰À˚“ÚÀÿ£¨…Ë‘⁄µ⁄
.≤ªøº¬«∆‰À˚“ÚÀÿ£¨…Ë‘⁄µ⁄![]() ƒÍƒ⁄”„»∫µƒ∑±÷≥¡øº∞≤∂¿Ã¡ø∂º”Î
ƒÍƒ⁄”„»∫µƒ∑±÷≥¡øº∞≤∂¿Ã¡ø∂º”Î![]() ≥…’˝±»£¨À¿Õˆ¡ø”Î
≥…’˝±»£¨À¿Õˆ¡ø”Î![]() ≥…’˝±»£¨’‚–©±»¿˝œµ ˝“¿¥ŒŒ™’˝≥£ ˝
≥…’˝±»£¨’‚–©±»¿˝œµ ˝“¿¥ŒŒ™’˝≥£ ˝![]() £¨
£¨![]() £¨
£¨![]()
£®1£©«Û![]() ”Î
”Î![]() µƒπÿœµ Ω
µƒπÿœµ Ω
£®2£©»Ù√øƒÍƒÍ≥ı”„»∫µƒ◊Сø±£≥÷≤ª±‰£¨«Û![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() À˘”¶¬˙◊„µƒÃıº˛
À˘”¶¬˙◊„µƒÃıº˛
£®3£©…Ë![]() £¨
£¨![]() £¨Œ™±£÷§∂‘»Œ“‚
£¨Œ™±£÷§∂‘»Œ“‚![]() £¨∂º”–
£¨∂º”–![]() £¨‘Ú≤∂¿Ã«ø∂»
£¨‘Ú≤∂¿Ã«ø∂»![]() µƒ◊Ó¥Û‘ –Ì÷µ «∂ý…Ÿ£ø≤¢Àµ√˜¿Ì”….
µƒ◊Ó¥Û‘ –Ì÷µ «∂ý…Ÿ£ø≤¢Àµ√˜¿Ì”….
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∫Ø ˝![]() £¨»Ù¥Ê‘⁄≥£ ˝
£¨»Ù¥Ê‘⁄≥£ ˝![]() £¨∂‘»Œ“‚
£¨∂‘»Œ“‚![]() ∂º”–
∂º”–![]() £¨‘Ú≥∆∫Ø ˝
£¨‘Ú≥∆∫Ø ˝![]() Œ™T±∂÷Ð∆⁄∫Ø ˝.
Œ™T±∂÷Ð∆⁄∫Ø ˝.
£®1£©≈–∂œ![]() «∑Ò «T±∂÷Ð∆⁄∫Ø ˝£¨≤¢Àµ√˜¿Ì”…£ª
«∑Ò «T±∂÷Ð∆⁄∫Ø ˝£¨≤¢Àµ√˜¿Ì”…£ª
£®2£©÷§√˜ «T±∂÷Ð∆⁄∫Ø ˝£¨«“Tµƒ÷µ «Œ®“ªµƒ£ª
«T±∂÷Ð∆⁄∫Ø ˝£¨«“Tµƒ÷µ «Œ®“ªµƒ£ª
£®3£©»Ù![]() «2±∂÷Ð∆⁄∫Ø ˝£¨
«2±∂÷Ð∆⁄∫Ø ˝£¨![]() £¨
£¨![]() £¨
£¨![]() ±Ì æ
±Ì æ![]() µƒ«∞nœÓ∫Õ£¨
µƒ«∞nœÓ∫Õ£¨![]() £¨»Ù
£¨»Ù![]() ∫„≥…¡¢£¨«Ûaµƒ»°÷µ∑∂Œß.
∫„≥…¡¢£¨«Ûaµƒ»°÷µ∑∂Œß.
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨∂ص„
÷–£¨∂ص„![]() µΩ∂®µ„
µΩ∂®µ„![]() µƒæý¿Î”ÎÀ¸µΩ÷±œþ
µƒæý¿Î”ÎÀ¸µΩ÷±œþ![]() µƒæý¿Îœýµ»£Æ
µƒæý¿Îœýµ»£Æ
£®1£©«Û∂ص„![]() µƒπϺ£
µƒπϺ£![]() µƒ∑Ω≥ãª
µƒ∑Ω≥ãª
£®2£©…Ë∂Ø÷±œþ![]() ”Ϋ˙œþ
”Ϋ˙œþ![]() œý«–”⁄µ„
œý«–”⁄µ„![]() £¨”Î÷±œþ
£¨”Î÷±œþ![]() œýΩª”⁄µ„
œýΩª”⁄µ„![]() £Æ
£Æ
÷§√˜£∫“‘![]() Œ™÷±æ∂µƒ‘≤∫„π˝
Œ™÷±æ∂µƒ‘≤∫„π˝![]() ÷·…œƒ≥∂®µ„£Æ
÷·…œƒ≥∂®µ„£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∫Ø ˝![]() ÕºœÛ…œ≤ªÕ¨¡Ωµ„
ÕºœÛ…œ≤ªÕ¨¡Ωµ„![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() ¥¶µƒ«–œþµƒ–±¬ ∑÷± «
¥¶µƒ«–œþµƒ–±¬ ∑÷± «![]() £¨
£¨![]() £¨πÊ∂®
£¨πÊ∂®![]() Ω–«˙œþ
Ω–«˙œþ![]() ‘⁄µ„
‘⁄µ„![]() ”ε„
”ε„![]() ÷ƺ‰µƒ°∞Õ‰«˙∂»°±£¨∏¯≥ˆ“‘œ¬√¸Ã‚£∫
÷ƺ‰µƒ°∞Õ‰«˙∂»°±£¨∏¯≥ˆ“‘œ¬√¸Ã‚£∫
£®1£©∫Ø ˝![]() ÕºœÛ…œ¡Ωµ„
ÕºœÛ…œ¡Ωµ„![]() °¢
°¢![]() µƒ∫·◊¯±Í∑÷±Œ™1£¨2£¨‘Ú
µƒ∫·◊¯±Í∑÷±Œ™1£¨2£¨‘Ú![]() £ª
£ª
£®2£©¥Ê‘⁄’‚—˘µƒ∫Ø ˝£¨ÕºœÛ…œ»Œ“‚¡Ωµ„÷ƺ‰µƒ°∞Õ‰«˙∂»°±Œ™≥£ ˝£ª
£®3£©…˵„![]() °¢
°¢![]() «≈◊ŒÔœþ£¨
«≈◊ŒÔœþ£¨![]() …œ≤ªÕ¨µƒ¡Ωµ„£¨‘Ú
…œ≤ªÕ¨µƒ¡Ωµ„£¨‘Ú![]() £ª
£ª
£®4£©…Ë«˙œþ![]() …œ≤ªÕ¨¡Ωµ„
…œ≤ªÕ¨¡Ωµ„![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨«“
£¨«“![]() £¨»Ù
£¨»Ù![]() ∫„≥…¡¢£¨‘Ú µ ˝
∫„≥…¡¢£¨‘Ú µ ˝![]() µƒ»°÷µ∑∂Œß «
µƒ»°÷µ∑∂Œß «![]() £ª
£ª
“‘…œ’˝»∑√¸Ã‚µƒ–Ú∫≈Œ™__£®–¥≥ˆÀ˘”–’˝»∑µƒ£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄Àƒ¿‚÷˘![]() ÷–£¨≤ý¿‚
÷–£¨≤ý¿‚![]() µ◊√Ê
µ◊√Ê![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() £¨£®
£¨£®![]() £©
£©
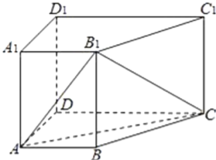
£®1£©«Û÷§£∫![]() ∆Ω√Ê
∆Ω√Ê![]() £ª
£ª
£®2£©»Ù÷±œþ![]() ”Î∆Ω√Ê
”Î∆Ω√Ê![]() À˘≥…Ω«µƒ’˝œ“÷µŒ™
À˘≥…Ω«µƒ’˝œ“÷µŒ™![]() £¨«Û
£¨«Û![]() µƒ÷µ£ª
µƒ÷µ£ª
£®3£©œ÷Ω´”ÎÀƒ¿‚÷˘![]() –Œ◊¥∫Õ¥Û–°ÕÍ»´œýÕ¨µƒ¡Ω∏ˆÀƒ¿‚÷˘∆¥≥…“ª∏ˆ–¬µƒÀƒ¿‚÷˘£¨πÊ∂®£∫»Ù∆¥≥…µƒ–¬Àƒ¿‚÷˘–Œ◊¥∫Õ¥Û–°ÕÍ»´œýÕ¨£¨‘Ú ”Œ™Õ¨“ª÷÷∆¥Ω”∑Ω∞∏£¨Œ π≤”–º∏÷÷≤ªÕ¨µƒ∆¥Ω”∑Ω∞∏£ø‘⁄’‚–©∆¥Ω”≥…µƒ–¬Àƒ¿‚÷˘÷–£¨º«∆‰÷–◊Ó–°µƒ±Ì√ʪ˝Œ™
–Œ◊¥∫Õ¥Û–°ÕÍ»´œýÕ¨µƒ¡Ω∏ˆÀƒ¿‚÷˘∆¥≥…“ª∏ˆ–¬µƒÀƒ¿‚÷˘£¨πÊ∂®£∫»Ù∆¥≥…µƒ–¬Àƒ¿‚÷˘–Œ◊¥∫Õ¥Û–°ÕÍ»´œýÕ¨£¨‘Ú ”Œ™Õ¨“ª÷÷∆¥Ω”∑Ω∞∏£¨Œ π≤”–º∏÷÷≤ªÕ¨µƒ∆¥Ω”∑Ω∞∏£ø‘⁄’‚–©∆¥Ω”≥…µƒ–¬Àƒ¿‚÷˘÷–£¨º«∆‰÷–◊Ó–°µƒ±Ì√ʪ˝Œ™![]() £¨–¥≥ˆ
£¨–¥≥ˆ![]() µƒΩ‚Œˆ Ω£Æ£®÷±Ω”–¥≥ˆ¥∞∏£¨≤ª±ÿÀµ√˜¿Ì”…£©
µƒΩ‚Œˆ Ω£Æ£®÷±Ω”–¥≥ˆ¥∞∏£¨≤ª±ÿÀµ√˜¿Ì”…£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄÷±Ω«◊¯±Íœµ![]() ÷–,∂‘”⁄µ„
÷–,∂‘”⁄µ„![]() ,∂®“±‰ªª
,∂®“±‰ªª![]() :Ω´µ„
:Ω´µ„![]() ±‰ªªŒ™µ„
±‰ªªŒ™µ„![]() , πµ√
, πµ√![]() ∆‰÷–
∆‰÷–![]() .’‚—˘±‰ªª
.’‚—˘±‰ªª![]() æÕΩ´◊¯±Íœµ
æÕΩ´◊¯±Íœµ![]() ƒ⁄µƒ«˙œþ±‰ªªŒ™◊¯±Íœµ
ƒ⁄µƒ«˙œþ±‰ªªŒ™◊¯±Íœµ![]() ƒ⁄µƒ«˙œþ.‘ÚÀƒ∏ˆ∫Ø ˝
ƒ⁄µƒ«˙œþ.‘ÚÀƒ∏ˆ∫Ø ˝![]() ,
,![]() ,
,![]() ,
,![]() ‘⁄◊¯±Íœµ
‘⁄◊¯±Íœµ![]() ƒ⁄µƒÕºœÛ,±‰ªªŒ™◊¯±Íœµ
ƒ⁄µƒÕºœÛ,±‰ªªŒ™◊¯±Íœµ![]() ƒ⁄µƒÀƒÃı«˙œþ£®»ÁÕº£©“¿¥Œ «
ƒ⁄µƒÀƒÃı«˙œþ£®»ÁÕº£©“¿¥Œ «

A. ¢⁄,¢€,¢Ÿ,¢ÐB. ¢€,¢⁄,¢Ð,¢ŸC. ¢⁄,¢€,¢Ð,¢ŸD. ¢€,¢⁄,¢Ÿ,¢Ð
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø
‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨“‘◊¯±Í‘≠µ„OŒ™º´µ„£¨x÷·’˝∞Î÷·Œ™º´÷·£¨Ω®¡¢º´◊¯±Íœµ£¨“—÷™«˙œþCµƒº´◊¯±Í∑Ω≥ÃŒ™£∫![]() £¨æ≠π˝µ„
£¨æ≠π˝µ„![]() £¨«„–±Ω«Œ™
£¨«„–±Ω«Œ™![]() µƒ÷±œþl”Ϋ˙œþCΩª”⁄A£¨B¡Ωµ„
µƒ÷±œþl”Ϋ˙œþCΩª”⁄A£¨B¡Ωµ„
£®I£©«Û«˙œþCµƒ÷±Ω«◊¯±Í∑Ω≥Ã∫Õ÷±œþlµƒ≤Œ ˝∑Ω≥ãª
£®¢Ú£©«Û![]() µƒ÷µ°£
µƒ÷µ°£
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
∞Ÿ∂»÷¬–≈ - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com