
【题目】已知函数![]() .
.
(1)若![]() 是
是![]() 的极值点,试研究函数
的极值点,试研究函数![]() 的单调性,并求
的单调性,并求![]() 的极值;
的极值;
(2)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)详见解析;(2)![]() .
.
【解析】试题分析:(1)现求![]() ,再由
,再由![]() 是
是![]() 的极值点,求得
的极值点,求得![]() 的值,最后根据
的值,最后根据![]() 得到函数
得到函数![]() 的单调性和极值;
的单调性和极值;
(2)将不等式的恒成立问题转化为求曲线![]() 的最小值问题,对
的最小值问题,对![]() 分类讨论,即可确定实数
分类讨论,即可确定实数![]() 的取值范围.
的取值范围.
试题解析:
(1)函数![]() ,定义域为
,定义域为![]() ,则
,则![]() ,
,
若![]() 是
是![]() 的极值点,则
的极值点,则![]() ,即
,即![]() .
.
∴![]() ,
, ![]() .
.
令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
,
∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 在
在![]() 处取得极小值,极小值为
处取得极小值,极小值为![]() .
.
(2)若![]() 在
在![]() 上恒成立,即
上恒成立,即![]() .
.
由(1)知![]() ,
,
(i)当![]() 时,即
时,即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上单调递减,
上单调递减,
则![]() ,得
,得![]() .
.
(ii)当![]() 时,
时, ![]() 时,
时, ![]() ,
,
![]() 时,
时, ![]() ,
,
若![]() ,即
,即![]() 时,
时, ![]() 在
在![]() 上恒成立,
上恒成立,
则![]() 在
在![]() 上单调递减,∴
上单调递减,∴![]() ,即
,即![]() 时
时![]() 恒成立,
恒成立,
若![]() ,即
,即![]() 时,
时, ![]() 时,
时, ![]() ,
, ![]() 时,
时, ![]() .
.
即![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
则![]() ,得
,得![]() .
.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
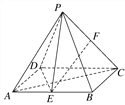
【题目】如图,四棱锥P-ABCD的底面为矩形,AB=![]() ,BC=1,E,F分别是AB,PC的中点,DE⊥PA.
,BC=1,E,F分别是AB,PC的中点,DE⊥PA.
(1)求证:EF∥平面PAD;
(2)求证:平面PAC⊥平面PDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x+1)e-x(e为自然对数的底数).
(1)求函数f(x)的单调区间;
(2)设函数φ(x)=xf(x)+tf′(x)+e-x,存在实数x1,x2∈[0,1],使得2φ(x1)<φ(x2)成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体![]() 中,
中, ![]() ,
, ![]() ,点
,点![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
, ![]() 的中点,过点
的中点,过点![]() 的平面
的平面![]() 与平面
与平面![]() 平行,且与长方体的面相交,交线围成一个几何图形.
平行,且与长方体的面相交,交线围成一个几何图形.
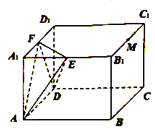
(1)在图中画出这个几何图形(说明画法,不需要说明理由);
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已经函数![]() 的定义域为
的定义域为![]() ,设
,设![]()
(1)试确定![]() 的取值范围,使得函数
的取值范围,使得函数![]() 在
在![]() 上为单调函数
上为单调函数
(2)求证![]()
(3)若不等式![]() (为
(为![]() 正整数)对任意正实数
正整数)对任意正实数![]() 恒成立,求
恒成立,求![]() 的最大值.(解答过程可参考使用以下数据
的最大值.(解答过程可参考使用以下数据![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】把2支相同的晨光签字笔,3支相同英雄钢笔全部分给4名优秀学生,每名学生至少1支,则不同的分法有( )
A. 24种 B. 28种 C. 32种 D. 36种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第三届移动互联创新大赛,于2017年3月~10月期间举行,为了选出优秀选手,某高校先在计算机科学系选出一种子选手![]() ,再从全校征集出3位志愿者分别与
,再从全校征集出3位志愿者分别与![]() 进行一场技术对抗赛,根据以往经验,
进行一场技术对抗赛,根据以往经验, ![]() 与这三位志愿者进行比赛一场获胜的概率分别为
与这三位志愿者进行比赛一场获胜的概率分别为![]() ,且各场输赢互不影响.
,且各场输赢互不影响.
(1)求甲恰好获胜两场的概率;
(2)求甲获胜场数的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某海产品经销商调查发现,该海产品每售出![]() 吨可获利
吨可获利![]() 万元,每积压
万元,每积压![]() 吨则亏损
吨则亏损![]() 万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
万元.根据往年的数据,得到年需求量的频率分布直方图如图所示,将频率视为概率.
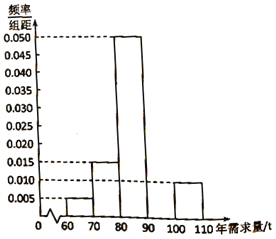
(1)请补齐![]() 上的频率分布直方图,并依据该图估计年需求量的平均数;
上的频率分布直方图,并依据该图估计年需求量的平均数;
(2)今年该经销商欲进货![]() 吨,以
吨,以![]() (单位:吨,
(单位:吨, ![]() )表示今年的年需求量,以
)表示今年的年需求量,以![]() (单位:万元)表示今年销售的利润,试将
(单位:万元)表示今年销售的利润,试将![]() 表示为
表示为![]() 的函数解析式;并求今年的年利润不少于
的函数解析式;并求今年的年利润不少于![]() 万元的概率.
万元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com