
ЎҫМвДҝЎҝДіТыБПЙъІъЖуТөОӘБЛХјУРёь¶аөДКРіЎ·Э¶оЈ¬ДвФЪ2017Дк¶ИҪшРРТ»ПөБРҙЩПъ»о¶ҜЈ¬ҫӯ№эКРіЎөчІйәНІвЛгЈ¬ТыБПөДДкПъКЫБҝxНтјюУлДкҙЩПъ·СtНтФӘјдВъЧг ![]() .ТСЦӘ2017ДкЙъІъТыБПөДЙиұёХЫҫЙЈ¬О¬РЮөИ№М¶Ё·СУГОӘ3НтФӘЈ¬ГҝЙъІъ1НтјюТыБПРиФЩН¶Ил32НтФӘөДЙъІъ·СУГЈ¬ИфҪ«ГҝјюТыБПөДКЫјЫ¶ЁОӘЖдЙъІъіЙұҫөД150%УлЖҪҫщГҝјюҙЩПъ·СөДТ»°лЦ®әНЈ¬ФтёГДкЙъІъөДТыБПХэәГДЬПъКЫНкЈ®
.ТСЦӘ2017ДкЙъІъТыБПөДЙиұёХЫҫЙЈ¬О¬РЮөИ№М¶Ё·СУГОӘ3НтФӘЈ¬ГҝЙъІъ1НтјюТыБПРиФЩН¶Ил32НтФӘөДЙъІъ·СУГЈ¬ИфҪ«ГҝјюТыБПөДКЫјЫ¶ЁОӘЖдЙъІъіЙұҫөД150%УлЖҪҫщГҝјюҙЩПъ·СөДТ»°лЦ®әНЈ¬ФтёГДкЙъІъөДТыБПХэәГДЬПъКЫНкЈ®
ЈЁ1Ј©Ҫ«2017ДкөДАыИуy(НтФӘ)ұнКҫОӘҙЩПъ·Сt(НтФӘ)өДәҜКэЈ»
ЈЁ2Ј©ёГЖуТө2017ДкөДҙЩПъ·СН¶Ил¶аЙЩНтФӘКұЈ¬ЖуТөөДДкАыИуЧоҙуЈҝ
(ЧўЈәАыИуЈҪПъКЫКХИлЈӯЙъІъіЙұҫЈӯҙЩПъ·СЈ¬ЙъІъіЙұҫЈҪ№М¶Ё·СУГЈ«ЙъІъ·СУГ)
Ўҫҙр°ёЎҝ
ЈЁ1Ј©ҪвЈәөұДкПъБҝОӘxНтјюКұЈ¬іЙұҫОӘ3Ј«32x(НтФӘ)Ј®
ТыБПөДКЫјЫОӘ ![]() ЎБ150%Ј«
ЎБ150%Ј« ![]() ЎБ
ЎБ ![]() (НтФӘ/Нтјю)Ј¬
(НтФӘ/Нтјю)Ј¬
ЛщТФДкАыИуyЈҪ ![]() xЈӯ(3Ј«32xЈ«t)(НтФӘ)Ј¬
xЈӯ(3Ј«32xЈ«t)(НтФӘ)Ј¬
°СxЈҪ ![]() ҙъИлХыАнөГөҪyЈҪ
ҙъИлХыАнөГөҪyЈҪ ![]() Ј¬ЖдЦРtЎЭ0.
Ј¬ЖдЦРtЎЭ0.
ЈЁ2Ј©ҪвЈәУЙ(1)ЦӘyЈҪ ![]() ЈҪ
ЈҪ ![]() ЈҪ50Јӯ
ЈҪ50Јӯ ![]() ЎЬ50Јӯ2
ЎЬ50Јӯ2 ![]() ЈҪ42(НтФӘ)Ј¬
ЈҪ42(НтФӘ)Ј¬
өұЗТҪцөұ ![]() ЈҪ
ЈҪ ![]() Ј¬јҙtЈҪ7КұЈ¬ymaxЈҪ42.
Ј¬јҙtЈҪ7КұЈ¬ymaxЈҪ42.
ЛщТФёГЖуТө2017ДкөДҙЩПъ·СН¶Ил7НтФӘКұЈ¬ЖуТөөДДкАыИуЧоҙуОӘ42НтФӘЈ®
ЎҫҪвОцЎҝЈЁ1Ј©И·¶ЁТыБПөДКЫјЫЈ¬јҙҝЙНЁ№эxұнКҫіцДкАыИуyЈ¬»ҜјтҙъИлХыАнјҙҝЙЗуіцyНтФӘұнКҫОӘҙЩПъ·СtНтФӘөДәҜКэЈ»
ЈЁ2Ј©ёщҫЭТСЦӘҙъИлЈЁ1Ј©өДәҜКэЈ¬·ЦұрҪшРР»ҜјтЈ¬АыУГ№ШУЪtөД·ҪіМұШРлУРБҪХэёщҪЁБў№ШПөКҪЈ¬ҝЙЗуіцЧоЦөЈ¬јҙҙЩПъ·СН¶Ил¶аЙЩНтФӘКұЈ¬ЖуТөөДДкАыИуЧоҙуЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЎчABCЦРЈ¬AC=2Ј¬A=120ЎгЈ¬ ![]() Ј®
Ј®
ЈЁўсЈ©ЗуұЯABөДіӨЈ»
ЈЁўтЈ©ЙиЈЁ3Ј¬4Ј©КЗBCұЯЙПТ»өгЈ¬ЗТЎчACDөДГж»эОӘ ![]() Ј¬ЗуЎПADCөДХэПТЦөЈ®
Ј¬ЗуЎПADCөДХэПТЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘөИСьМЭРОABCDЦРABЎОCDЈ¬AB=2CD=4Ј¬ЎПBAD=60ЎгЈ¬Л«ЗъПЯТФAЈ¬BОӘҪ№өгЈ¬ЗТУлПЯ¶ОCDЈЁ°ьАЁ¶ЛөгCЎўDЈ©УРБҪёцҪ»өгЈ¬ФтёГЛ«ЗъПЯөДАлРДВКөДИЎЦө·¶О§КЗ Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪКэБР{an}ј°{bn}ЦРЈ¬an+1=an+bn+ ![]() =1Ј®Йи
=1Ј®Йи ![]() Ј¬ФтКэБР{cn}өДЗ°nПоәНОӘЈЁЎЎЎЎЈ©
Ј¬ФтКэБР{cn}өДЗ°nПоәНОӘЈЁЎЎЎЎЈ©
A.![]()
B.2n+2©Ғ4
C.3ЎБ2n+2n©Ғ4
D.![]()
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЦұҪЗЧшұкПөxOyЦРЈ¬ЗъПЯC1өДІОКэ·ҪіМКЗ 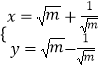 ЈЁmОӘІОКэЈ©Ј¬ЦұПЯlҪ»ЗъПЯC1УЪAЈ¬BБҪөгЈ»ТФЧшұкФӯөгОӘј«өгЈ¬xЦбөДХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯC2өДј«Чшұк·ҪіМКЗҰС=4sinЈЁҰИ©Ғ
ЈЁmОӘІОКэЈ©Ј¬ЦұПЯlҪ»ЗъПЯC1УЪAЈ¬BБҪөгЈ»ТФЧшұкФӯөгОӘј«өгЈ¬xЦбөДХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯC2өДј«Чшұк·ҪіМКЗҰС=4sinЈЁҰИ©Ғ ![]() Ј©Ј¬өгPЈЁҰСЈ¬
Ј©Ј¬өгPЈЁҰСЈ¬ ![]() Ј©ФЪЗъПЯC2ЙПЈ®
Ј©ФЪЗъПЯC2ЙПЈ®
ЈЁ1Ј©ЗуЗъПЯC1өДЖХНЁ·ҪіМј°өгPөДЦұҪЗЧшұкЈ»
ЈЁ2Ј©ИфЦұПЯlөДЗгРұҪЗОӘ ![]() ЗТҫӯ№эөгPЈ¬Зу|PA|+|PB|өДЦөЈ®
ЗТҫӯ№эөгPЈ¬Зу|PA|+|PB|өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘФІ ![]() Јә
Јә ![]() ЈЁ
ЈЁ ![]() Ј©УлЦұПЯ
Ј©УлЦұПЯ ![]() Јә
Јә ![]() ПаЗРЈ¬Йиөг
ПаЗРЈ¬Йиөг ![]() ОӘФІЙПТ»¶ҜөгЈ¬
ОӘФІЙПТ»¶ҜөгЈ¬ ![]() ЦбУЪ
ЦбУЪ ![]() Ј¬ЗТ¶Ҝөг
Ј¬ЗТ¶Ҝөг ![]() ВъЧг
ВъЧг ![]() Ј¬Йи¶Ҝөг
Ј¬Йи¶Ҝөг ![]() өД№мјЈОӘЗъПЯ
өД№мјЈОӘЗъПЯ ![]() Ј®
Ј®
ЈЁ1Ј©ЗуЗъПЯ ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©ЦұПЯ ![]() УлЦұПЯ
УлЦұПЯ ![]() ҙ№ЦұЗТУлЗъПЯ
ҙ№ЦұЗТУлЗъПЯ ![]() Ҫ»УЪ
Ҫ»УЪ ![]() Ј¬
Ј¬ ![]() БҪөгЈ¬Зу
БҪөгЈ¬Зу ![]() Гж»эөДЧоҙуЦөЈ®
Гж»эөДЧоҙуЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ ![]() Ј¬
Ј¬ ![]() Ј®
Ј®
ЈЁ1Ј©ЗуәҜКэ ![]() өДөҘөчФцЗшјдЈ»
өДөҘөчФцЗшјдЈ»
ЈЁ2Ј©Иф ![]() Ј¬ҪвІ»өИКҪ
Ј¬ҪвІ»өИКҪ ![]() Ј»
Ј»
ЈЁ3Ј©Иф ![]() Ј¬ЗТ¶ФИОТв
Ј¬ЗТ¶ФИОТв ![]() Ј¬·ҪіМ
Ј¬·ҪіМ ![]() ФЪ
ФЪ ![]() ЧЬҙжФЪБҪІ»ПаөИөДКөКэёщЈ¬Зу
ЧЬҙжФЪБҪІ»ПаөИөДКөКэёщЈ¬Зу ![]() өДИЎЦө·¶О§Ј®
өДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝјЧЎўТТЎўұыЎў¶ЎЛДО»Н¬С§Т»ЖрИҘПтАПКҰСҜОКіЙУпҫәИьөДіЙјЁЈ¬АПКҰЛөЈ¬ДгГЗЛДИЛЦРУР2О»УЕРгЈ¬2О»БјәГЈ¬ОТПЦФЪёшјЧҝҙТТЎўұыөДіЙјЁЈ¬ёшТТҝҙұыөДіЙјЁЈ¬ёш¶ЎҝҙјЧөДіЙјЁЈ¬ҝҙәујЧ¶ФҙујТЛөЈәОТ»№КЗІ»ЦӘөАОТөДіЙјЁЈ¬ёщҫЭТФЙПРЕПўЈ¬ФтЈЁ Ј©
A.ТТҝЙТФЦӘөАБҪИЛөДіЙјЁ
B.¶ЎҝЙДЬЦӘөАБҪИЛөДіЙјЁ
C.ТТЎў¶ЎҝЙТФЦӘөА¶Ф·ҪөДіЙјЁ
D.ТТЎў¶ЎҝЙТФЦӘөАЧФјәөДіЙјЁ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝФЪЖҪГжЦұҪЗЧшұкПө ![]() ЦРЈ¬ТФЧшұкФӯөгОӘј«өгЈ¬
ЦРЈ¬ТФЧшұкФӯөгОӘј«өгЈ¬ ![]() ЦбХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПө. ЗъПЯ
ЦбХэ°лЦбОӘј«ЦбҪЁБўј«ЧшұкПө. ЗъПЯ ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ ![]() Ј¬
Ј¬ ![]() ОӘЗъПЯ
ОӘЗъПЯ ![]() ЙПТмУЪј«өгөД¶ҜөгЈ¬өг
ЙПТмУЪј«өгөД¶ҜөгЈ¬өг ![]() ФЪЙдПЯ
ФЪЙдПЯ ![]() ЙПЈ¬ЗТ
ЙПЈ¬ЗТ ![]() іЙөИұИКэБРЈ®
іЙөИұИКэБРЈ®
ЈЁўсЈ©Зуөг ![]() өД№мјЈ
өД№мјЈ ![]() өДЦұҪЗЧшұк·ҪіМЈ»
өДЦұҪЗЧшұк·ҪіМЈ»
ЈЁўтЈ©ТСЦӘ ![]() ,
, ![]() КЗЗъПЯ
КЗЗъПЯ ![]() ЙПөДТ»өгЗТәбЧшұкОӘ
ЙПөДТ»өгЗТәбЧшұкОӘ ![]() Ј¬ЦұПЯ
Ј¬ЦұПЯ ![]() Ул
Ул ![]() Ҫ»УЪ
Ҫ»УЪ ![]() БҪөгЈ¬КФЗу
БҪөгЈ¬КФЗу ![]() өДЦөЈ®
өДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
°Щ¶ИЦВРЕ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com