
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度后得到函数
个单位长度后得到函数![]() 的图象,
的图象,![]() 分别是
分别是![]() 的极值点,且有
的极值点,且有![]() ,则函数
,则函数![]() ( )
( )
A.在区间![]() 上单调递增B.在区间
上单调递增B.在区间![]() 上单调递增
上单调递增
C.在区间![]() 上单调递减D.在区间
上单调递减D.在区间![]() 上单调递减
上单调递减
【答案】D
【解析】
先得到![]() 的一个极值大点,然后根据
的一个极值大点,然后根据![]() ,得到
,得到![]() 的一个极大值点或极小值点,分别得到
的一个极大值点或极小值点,分别得到![]() ,再得到
,再得到![]() 的解析式,再分别求出其单调区间,判断四个选项是否符合,从而得到答案.
的解析式,再分别求出其单调区间,判断四个选项是否符合,从而得到答案.
![]() ,可知
,可知![]() 是其一个极值点,
是其一个极值点,
![]() ,
,
因为![]() 分别是
分别是![]() 的极值点,且有
的极值点,且有![]() ,
,
所以![]() 的一个极大值点为
的一个极大值点为![]() ,
,
或者![]() 的一个极小值点为
的一个极小值点为![]() ,
,
①![]() 的一个极大值点为
的一个极大值点为![]() 时,
时,
代入到![]() ,得
,得![]() ,
,
即![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,
![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
所以![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() ,
,
因此可得,![]() 在区间
在区间![]() 上单调递减,选项D符合.
上单调递减,选项D符合.
②![]() 的一个极小值点为
的一个极小值点为![]() 时,
时,
代入到![]() ,得
,得![]() ,
,
即![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,
![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
所以![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
所以![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() ,
,
所以这种情况下,没有选项符合.
故选:D.


科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求出![]() ,
,![]() ,
,![]() 的值,并求出
的值,并求出![]() 及数列
及数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,在数列
,在数列![]() 中取出
中取出![]() (
(![]() 且
且![]() )项,按照原来的顺序排列成一列,构成等比数列
)项,按照原来的顺序排列成一列,构成等比数列![]() ,若对任意的数列
,若对任意的数列![]() ,均有
,均有![]() ,试求
,试求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() .已知函数
.已知函数![]() ,
,![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)已知函数![]() 和
和![]() 的图象在公共点(x0,y0)处有相同的切线,
的图象在公共点(x0,y0)处有相同的切线,
(i)求证:![]() 在
在![]() 处的导数等于0;
处的导数等于0;
(ii)若关于x的不等式![]() 在区间
在区间![]() 上恒成立,求b的取值范围.
上恒成立,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种“笼具”由内,外两层组成,无下底面,内层和外层分别是一个圆锥和圆柱,其中圆柱与圆锥的底面周长相等,圆柱有上底面,制作时需要将圆锥的顶端剪去,剪去部分和接头忽略不计,已知圆柱的底面周长为![]() ,高为
,高为![]() ,圆锥的母线长为
,圆锥的母线长为![]() .
.
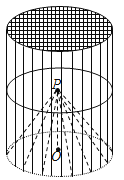
(1)求这种“笼具”的体积(结果精确到0.1![]() );
);
(2)现要使用一种纱网材料制作50个“笼具”,该材料的造价为每平方米8元,共需多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】经过多年的运作,“双十一”抢购活动已经演变成为整个电商行业的大型集体促销盛宴.为迎接2018年“双十一”网购狂欢节,某厂家拟投入适当的广告费,对网上所售产品进行促销.经调查测算,该促销产品在“双十一”的销售量p万件与促销费用x万元满足![]() (其中
(其中![]() ,a为正常数).已知生产该产品还需投入成本
,a为正常数).已知生产该产品还需投入成本![]() 万元(不含促销费用),每一件产品的销售价格定为
万元(不含促销费用),每一件产品的销售价格定为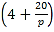 元,假定厂家的生产能力完全能满足市场的销售需求.
元,假定厂家的生产能力完全能满足市场的销售需求.
(1)将该产品的利润y万元表示为促销费用x万元的函数;
(2)促销费用投入多少万元时,厂家的利润最大?并求出最大利润的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com