
【题目】如图,在三棱锥![]() ,
,![]() 平面
平面![]() ,已知
,已知![]() ,点
,点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点.
的中点.

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 在线段
在线段![]() 上,满足
上,满足![]() 平面
平面![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见详解;(2)![]()
【解析】
(1)通过证明AD![]() PB,AD
PB,AD![]() BC,即可证明AD
BC,即可证明AD![]() 平面PBC;
平面PBC;
(2)通过构造面面平行,从而推出线线平行,再利用三角形相似求解.
(1)证明:因为BC![]() 平面PAB,AD
平面PAB,AD![]() 平面PAB,故:
平面PAB,故:
BC![]() AD;①
AD;①
又![]() 为等腰三角形,且D为PB中点,故:
为等腰三角形,且D为PB中点,故:
PB![]() AD;②
AD;②
又BC![]() 平面PBC,PB
平面PBC,PB![]() 平面PBC,
平面PBC,![]() ,结合①②,故:
,结合①②,故:
AD![]() 平面PBC,即证.
平面PBC,即证.
(2)取BE中点为M,连接DM、AM,作图如下:
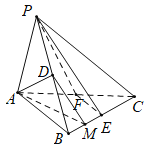
在![]() 中,因为D、M分别为PB、BE中点,故:
中,因为D、M分别为PB、BE中点,故:
DM//PE,又PE![]() 平面PEF,DM
平面PEF,DM![]() 平面PEF,故:
平面PEF,故:
DM//平面PEF,由已知得:AD//平面PEF,且
![]() ,DM
,DM![]() 平面ADM,AD
平面ADM,AD![]() 平面ADM,故:
平面ADM,故:
平面ADM//平面PEF;
又平面![]() 平面ADM
平面ADM![]() ,
,
平面ABC![]() 平面PEF
平面PEF![]() ,
,
故:AM//EF,则![]() ,
,![]() ;
;
因为:![]() ,故
,故![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某沿海地区的海岸线为一段圆弧![]() ,对应的圆心角
,对应的圆心角![]() ,该地区为打击走私,在海岸线外侧
,该地区为打击走私,在海岸线外侧![]() 海里内的海域
海里内的海域![]() 对不明船只进行识别查证(如图:其中海域与陆地近似看作在同一平面内),在圆弧的两端点
对不明船只进行识别查证(如图:其中海域与陆地近似看作在同一平面内),在圆弧的两端点![]() 、
、![]() 分别建有监测站,
分别建有监测站,![]() 与
与![]() 之间的直线距离为
之间的直线距离为![]() 海里.
海里.
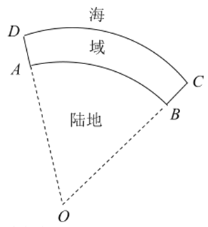
(1)求海域![]() 的面积;
的面积;
(2)现海上![]() 点处有一艘不明船只,在
点处有一艘不明船只,在![]() 点测得其距
点测得其距![]() 点
点![]() 海里,在
海里,在![]() 点测得其距
点测得其距![]() 点
点![]() 海里.判断这艘不明船只是否进入了海域
海里.判断这艘不明船只是否进入了海域![]() ?请说明理由.
?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知样本
10.1 | 8.7 | 6.4 | 10.5 | 13.0 | 8.3 | 10.0 | 12.4 |
8.0 | 9.0 | 11.2 | 9.3 | 12.7 | 9.6 | 10.6 | 11.0 |
那么其![]() 分位数和
分位数和![]() 分位数分别是( )
分位数分别是( )
A.![]() 和
和![]() B.
B.![]() 和
和![]() C.
C.![]() 和
和![]() D.
D.![]() 和
和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分14分)围建一个面积为![]() 的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽
的矩形场地,要求矩形场地的一面利用旧墙(利用的旧墙需维修,可供利用的旧墙足够长),其他三面围墙要新建,在旧墙对面的新墙上要留一个宽![]() 的进出口,如图2所示.已知旧墙的维修费用为
的进出口,如图2所示.已知旧墙的维修费用为![]() ,新墙的造价为
,新墙的造价为![]() .设利用旧墙的长度为
.设利用旧墙的长度为![]() (单位:
(单位:![]() ),修建此矩形场地围墙的总费用为
),修建此矩形场地围墙的总费用为![]() (单位:元).
(单位:元).

(1)将![]() 表示为
表示为![]() 的函数,并写出此函数的定义域;
的函数,并写出此函数的定义域;
(2)若要求用于维修旧墙的费用不得超过修建此矩形场地围墙的总费用的15%,试确定![]() ,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
,使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com