
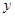 (万元)与处理量
(万元)与处理量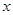 (吨)之间的函数关系可近似的表示为:
(吨)之间的函数关系可近似的表示为: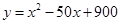 ,且每处理一吨废弃物可得价值为
,且每处理一吨废弃物可得价值为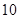 万元的某种产品,同时获得国家补贴
万元的某种产品,同时获得国家补贴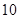 万元.
万元.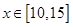 时,判断该项举措能否获利?如果能获利,求出最大利润;
时,判断该项举措能否获利?如果能获利,求出最大利润;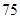 万元,该工厂才能不会亏损;(2)30.
万元,该工厂才能不会亏损;(2)30. 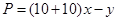 ,化简后它是关于
,化简后它是关于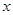 的二次函数,利用二次函数的知识求出
的二次函数,利用二次函数的知识求出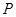 的取值范围,如果
的取值范围,如果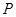 有非负的取值,就能说明可能获利,如果
有非负的取值,就能说明可能获利,如果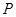 没有非负取值,说明不能获利,而国家最小补贴就是
没有非负取值,说明不能获利,而国家最小补贴就是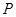 中最大值的绝对值. (2)每吨平均成本等于
中最大值的绝对值. (2)每吨平均成本等于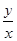 ,由题意
,由题意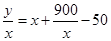 ,我们根据基本不等式的知识就可以求出它的最小值以及取最小值时的
,我们根据基本不等式的知识就可以求出它的最小值以及取最小值时的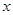 值.
值. 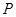 和处理量
和处理量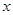 之间的关系:
之间的关系: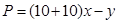
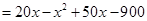
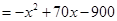 2分
2分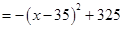 ,
,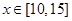 .
. 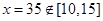 ,
,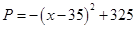 在
在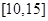 上为增函数,
上为增函数,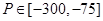 . 5分
. 5分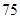 万元,该工厂就不会亏损. 7分
万元,该工厂就不会亏损. 7分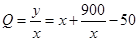 9分
9分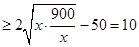 11分
11分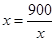 时等号成立,由
时等号成立,由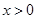 得
得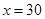 .
.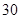 吨时,每吨的处理成本最少为
吨时,每吨的处理成本最少为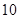 万元. 14分
万元. 14分

 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源:不详 题型:解答题
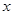 万件与年广告费用
万件与年广告费用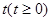 万元满足关系式:
万元满足关系式: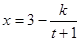 (
(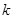 为常数).若不做广告,则产品的年销售量恰好为1万件.已知2014年生产该产品时,该厂需要先固定投入8万元,并且预计生产每1万件该产品时,需再投入4万元,每件产品的销售价格定为每件产品所需的年平均成本的1.5倍(每件产品的成本包括固定投入和生产再投入两部分,不包括广告促销费用).
为常数).若不做广告,则产品的年销售量恰好为1万件.已知2014年生产该产品时,该厂需要先固定投入8万元,并且预计生产每1万件该产品时,需再投入4万元,每件产品的销售价格定为每件产品所需的年平均成本的1.5倍(每件产品的成本包括固定投入和生产再投入两部分,不包括广告促销费用). (万元)表示为年广告促销费用
(万元)表示为年广告促销费用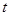 (万元)的函数;
(万元)的函数;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 对任意
对任意 都满足
都满足 ,且
,且 ,数列
,数列 满足:
满足: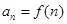 ,
,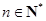 .
. 及
及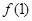 的值;
的值; 的通项公式;
的通项公式;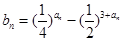 ,试问数列
,试问数列 是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.
是否存在最大项和最小项?若存在,求出最大项和最小项;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com