
 本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.
本题满分14分)本题共有2个小题,第1小题满分8分,第2小题满分6分.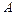 ,
,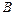 ,
,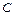 为△ABC的三个内角,向量
为△ABC的三个内角,向量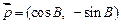 ,
,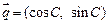 ,且
,且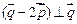 .
.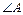 的大小;
的大小;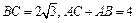 ,求△ABC的面积.
,求△ABC的面积.科目:高中数学 来源:不详 题型:解答题
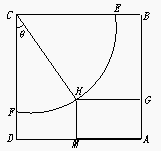
 某体育馆拟用运动场的边角地建一个矩形的健身室
某体育馆拟用运动场的边角地建一个矩形的健身室 (如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少?
(如图所示),ABCD是一块边长为50 m的正方形地皮,扇形CEF是运动场的一部分,其半径为40 m,矩形AGHM就是拟建的健身室,其中G、M分别在AB和AD上,H在 上。设矩形AGHM的面积为S,∠HCF=θ,请将S表示为θ的函数,并指出当点H在 的何处时,该健身室的面积最大,最大面积是多少? 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
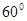 的方向,两船相距
的方向,两船相距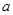 海里,乙船正在向北行驶,若甲船的速度是乙船的
海里,乙船正在向北行驶,若甲船的速度是乙船的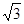 倍,甲船为了尽快追上乙船,应取北偏东
倍,甲船为了尽快追上乙船,应取北偏东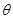 方向前进,则
方向前进,则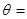
A.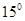 | B.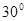 |
C.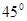 | D.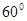 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com