
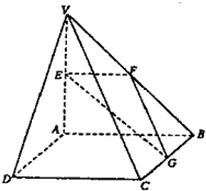
 如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点.
如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点.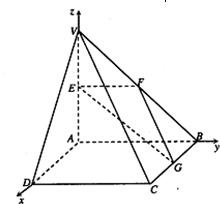 解:(I)∵E、F、G分别为VA、VB、BC的中点,∴EF∥AB,FG∥VC,
解:(I)∵E、F、G分别为VA、VB、BC的中点,∴EF∥AB,FG∥VC,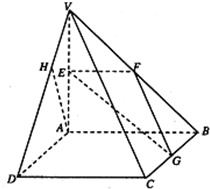
 VA
VA VA
VA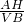 =
= …(11分)
…(11分) …(12分)
…(12分) ,
, ,0,0),C(
,0,0),C( ,1,0)
,1,0) =(x,y,z),
=(x,y,z), =(0,1,0),
=(0,1,0), =(
=( ,1,-1),
,1,-1),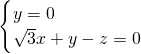
 =(1,0,
=(1,0, )为平面EFG的一个法向量
)为平面EFG的一个法向量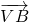 =(0,1,-1)则sinθ=|cos<
=(0,1,-1)则sinθ=|cos<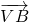 ,
, >=
>=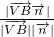 =
= …(11分)
…(11分) …(12分)
…(12分) ,我们分别求出直线VB的方向向量和平面EFG的一个法向量,代入向量夹角公式,即可得到直线VB与平面EFG所成的角.
,我们分别求出直线VB的方向向量和平面EFG的一个法向量,代入向量夹角公式,即可得到直线VB与平面EFG所成的角.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
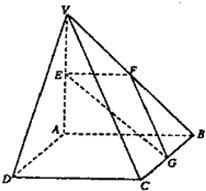 如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点.
如图,在四棱锥V-ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
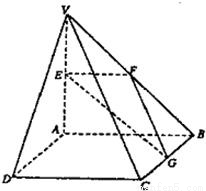
(本小题满分12分)如图,在四棱锥V—ABCD中,底面ABCD是矩形,侧棱VA⊥底面ABCD,E、F、G分别为VA、VB、BC的中点。(I)求证:平面EFG//平面VCD; (II)当二面角V—BC—A、V—DC—A分别为45°、30°时,求直线VB与平面EFG所成的角。
查看答案和解析>>
科目:高中数学 来源:2010年河北省唐山市高考数学一模试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2010年河北省唐山市高考数学一模试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com