
如图,有一块半椭圆形钢板,其长半轴长为 ,短半轴长为
,短半轴长为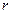 ,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记
,计划将此钢板切割成等腰梯形的形状,下底AB是半椭圆的短轴,上底CD的端点在椭圆上,记 ,梯形面积为S.
,梯形面积为S.
(1) 求面积S以
求面积S以 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;
(2)求面积S的最大值.
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=|x-a|.
(Ⅰ)若不等式f(x)≥3的解集为{x|x≤1或x≥5},求实数a的值;
(Ⅱ)在(Ⅰ)的条件下,若f(x)+f(x+4)≥m对一切实数x恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
据预测,我国在“十二五”期间内某产品关税与市场供应量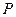 的关系近似地满足
的关系近似地满足 :
: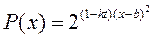 (其中
(其中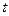 为关税的税率,且
为关税的税率,且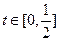 ,
,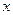 为市场价格,
为市场价格,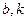 为正常数),当
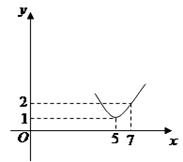
为正常数),当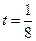 时的市场供应量曲线如图所示;
时的市场供应量曲线如图所示;
(1)根据图象求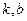 的值;
的值;
(2)若市场需求量为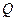 ,它近似满足
,它近似满足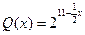 .
.
当 时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率
时的市场价格称为均衡价格,为使均衡价格控制在不低于9元的范围内,求税率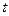 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知函数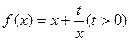 和点
和点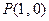 ,过点
,过点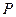 作曲线
作曲线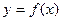 的两条切线
的两条切线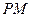 、
、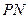 ,切点分别为
,切点分别为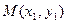 、
、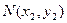 .
.
(1)求证: 为关于
为关于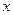 的方程
的方程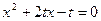 的两根;
的两根;
(2)设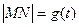 ,求函数
,求函数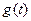 的表达式;
的表达式;
(3)在(2)的条件下,若在区间 内总存在
内总存在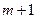 个实数
个实数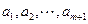 (可以相同),使得不等式
(可以相同),使得不等式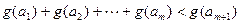 成立,求
成立,求 的最大值.
的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com