
【题目】已知函数![]() 为
为![]() 上的偶函数,
上的偶函数,![]() 为
为![]() 上的奇函数,且
上的奇函数,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若函数![]() 在
在![]() 上只有一个零点,求实数
上只有一个零点,求实数![]() 的取值范围.
的取值范围.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案科目:高中数学 来源: 题型:
【题目】假定小麦基本苗数![]() 与成熟期有效穗
与成熟期有效穗![]() 之间存在相关关系,今测得5组数据如下:
之间存在相关关系,今测得5组数据如下:

(1)以![]() 为解释变量,
为解释变量,![]() 为预报变量,画出散点图
为预报变量,画出散点图
(2)求![]() 与
与![]() 之间的回归方程
之间的回归方程
(3)当基本苗数为![]() 时预报有效穗(注:
时预报有效穗(注: ,
, ![]() )
)![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查某生产线上质量监督员甲是否在现场对产品质量好坏有无影响,现统计数据如下:质量监督员甲在现场时,1 000件产品中合格品有990件,次品有10件,甲不在现场时,500件产品中有合格品490件,次品有10件.
(1)补充下面列联表,并初步判断甲在不在现场与产品质量是否有关:
合格品数/件 | 次品数/件 | 总数/件 | |
甲在现场 | 990 | ||
甲不在现场 | 10 | ||
总数/件 |
(2)用独立性检验的方法判断能否在犯错误的概率不超过0.15的前提下认为“甲在不在现场与产品质量有关”?
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
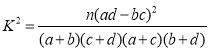
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数不超过20人,每人需交费用800元;若旅行团人数超过20人,则给予优惠:每多1人,人均费用减少10元,直到达到规定人数60人为止.旅行社需支付各种费用共计10000元.
(1)写出每人需交费用S关于旅行团人数![]() 的函数;
的函数;
(2)旅行团人数x为多少时,旅行社可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系
轴的正半轴为极轴建立极坐标系![]() ,点A为曲线
,点A为曲线![]() 上的动点,点B在线段OA的延长线上,且满足
上的动点,点B在线段OA的延长线上,且满足![]() ,点B的轨迹为
,点B的轨迹为![]() .
.
(1)求![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)设点C的极坐标为(2,0),求△ABC面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)的定义域是(0,+∞),且对任意正实数x,y都有f(xy)=f(x)+f(y)恒成立,已知f(2)=1,且x>1时,f(x)>0.
(1)求f(![]() )的值;
)的值;
(2)判断y=f(x)在(0,+∞)上的单调性并给出证明;
(3)解不等式f(2x)>f(8x-6)-1.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com