
已知异面直线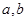 分别在平面
分别在平面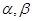 内,且平面
内,且平面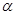 与
与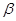 的交线为
的交线为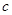 ,则直线
,则直线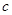 与
与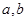 的位置关系是
的位置关系是
A.与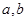 都平行 都平行 | B.至多与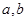 中的一条相交 中的一条相交 |
C.与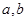 都不平行 都不平行 | D.至少与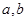 中的一条相交 中的一条相交 |
D
解析考点:空间中直线与直线之间的位置关系.
专题:探究型.
分析:由平行公理,我们可以判断A,D的正误,根据异面直线判定定理,可以判断B的正误,根据异面直线夹角的定义中平移直线法,可以判断C的正误,进而得到答案.
解答:解:若直线c与a,b均平行,由平行公理,可得a∥b,这与a,b异面矛盾,故A错误;
当a,b与c相交,但交点不同为一点时,a,b异面,故B错误;
如果a,b与c一条平行,一条相交,a,b异面,故C错误;
但如果c与a,b均不相交,则直线c与a,b均平行,由A中结论,可得假设不成立,故D正确;
故选D
点评:本题考查的知识点是空间中直线与直线之间的位置关系,其中熟练掌握空间直线不同位置关系的定义及几何特征是解答本题的关键.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源:2011年浙江省杭州市高二上学期期末考试数学文卷 题型:选择题
已知异面直线 分别在平面
分别在平面 内,且平面
内,且平面 与
与 的交线为
的交线为 ,则直线
,则直线 与
与 的位置关系是
的位置关系是
A.与 都平行 B.至多与
都平行 B.至多与 中的一条相交
中的一条相交
C.与 都不平行 D.至少与
都不平行 D.至少与 中的一条相交
中的一条相交
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com