
����Ŀ��Ϊ�Ƶ���������ʽ������������һ��IJ�Ϸ��ǣ���һ�������������������ഹֱ������Բ����������Բ���Ĺ������ֽ���IJ�Ϸ��ǣ�����û�еõ�IJ�Ϸ��ǵ������200����敜����IJ�Ϸ��ǵ�������㷽��������Ĺ��̱����˳�Ϊ�敜ԭ����Ե���Ƽ�ͬ����������죮��˼�ǣ���������ƽ��ƽ�������������屻ƽ����������ƽ��ƽ�������ƽ�����أ����������������ȣ���ô����������������Ҳ��ȣ����ڽ�ȡIJ�Ϸ��ǵİ˷�֮һ����������������![]() ���ⳤΪ1����ͼ��ʾ������������Ϣ�����IJ�Ϸ��ǵ����Ϊ�� ��
���ⳤΪ1����ͼ��ʾ������������Ϣ�����IJ�Ϸ��ǵ����Ϊ�� ��
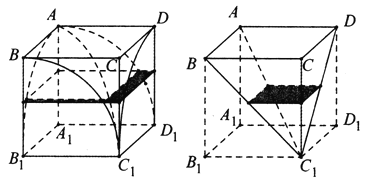
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
���𰸡�B
���������������ڸ߶�![]() ���Ľ��棬��ƽ�������������µ����ƽ��ȥ�أ��ǽص���Բ���幫�������������Ϊ
���Ľ��棬��ƽ�������������µ����ƽ��ȥ�أ��ǽص���Բ���幫�������������Ϊ![]() ���ص��������������Ϊ
���ص��������������Ϊ![]() ��������������Ϊ
��������������Ϊ![]() ��
��![]() ��
��
![]() �����
�����![]() �����ɶ�����������������������������ȥ���������.
�����ɶ�����������������������������ȥ���������.
��⣺�ڸ߶�![]() ���Ľ��棬��ƽ�������������µ����ƽ��ȥ�أ�
���Ľ��棬��ƽ�������������µ����ƽ��ȥ�أ�
�ǽص���Բ���幫�������������Ϊ![]() ���ص��������������Ϊ
���ص��������������Ϊ![]() ��
��
�ɵ�![]() ��
��![]() ��
��
��![]() ���ɵ�
���ɵ�![]() ����
����![]() ��
��
���Ը�IJ�Ϸ��ǵ����Ϊ![]() ����ѡB.
����ѡB.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
��![]() ��
��![]() ��
��![]() Ϊ
Ϊ![]() �е�.
�е�.
��1��֤����![]() ƽ��
ƽ��![]() ��
��
��2����![]() ƽ��
ƽ��![]() ��
��![]() �DZ߳�Ϊ2���������Σ����
�DZ߳�Ϊ2���������Σ����![]() ��ƽ��
��ƽ��![]() �ľ���.
�ľ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�M��N��E��F�ֱ�����A1B1��A1D1��B1C1��C1D1���е㣬��֤��ƽ��AMN��ƽ��EFDB��
�У�M��N��E��F�ֱ�����A1B1��A1D1��B1C1��C1D1���е㣬��֤��ƽ��AMN��ƽ��EFDB��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ķ�չ������ѧϰ��Ϊ��Ҫ������֪ʶҪ���£�ѧϰ��ѵ�ز����٣���ij�����й���1000��������250�����˲μӶ�����ѵ����Ϊ![]() ��ˣ�������750�����˲μӹ�������ѵ����Ϊ
��ˣ�������750�����˲μӹ�������ѵ����Ϊ![]() ��ˣ����Ӹù����Ĺ����й������100�����ˣ��������ǵ������������˴���������ָһ��ӹ�����������õ�
��ˣ����Ӹù����Ĺ����й������100�����ˣ��������ǵ������������˴���������ָһ��ӹ�����������õ�![]() ������������ľ�Ҷͼ����ͼ����
������������ľ�Ҷͼ����ͼ����![]() �������������Ƶ�ʷֲ�ֱ��ͼ����ͼ��.
�������������Ƶ�ʷֲ�ֱ��ͼ����ͼ��.

(1)��![]() �ࡢ
�ࡢ![]() ��˸�����˶��ٹ��ˣ������ֱ��ͼ�е�
��˸�����˶��ٹ��ˣ������ֱ��ͼ�е�![]() ��
��
(2)��![]() ������������������������
���������������λ����������![]() �������������ƽ������ͬһ���е������ø���������е�ֵ����������
�������������ƽ������ͬһ���е������ø���������е�ֵ����������
(3)���涨����������![]() ��Ϊ�������㣬������ͳ�������ڴ������������
��Ϊ�������㣬������ͳ�������ڴ������������![]() �����������ж��Ƿ�����ڷ�������ʲ�����0.1%��ǰ���£���Ϊ������������ѵʱ�䳤���й�.��������ѵʱ��������
�����������ж��Ƿ�����ڷ�������ʲ�����0.1%��ǰ���£���Ϊ������������ѵʱ�䳤���й�.��������ѵʱ��������
������ѵ | ������ѵ | �ϼ� | |
�������� | |||
���������� | |||
�ϼ� |
�ο����ݣ�
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�ο���ʽ��![]() ������
������![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC����a=7��b=8��cosB= �C![]() ��
��
����������A��
��������AC���ϵĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ��ֳ������ijˮ��Ʒ���¡���������ֳ�����IJ����Աȣ��ջ�ʱ�������ȡ��100�����䣬��������ˮ��Ʒ�IJ�������λ��kg��, ��Ƶ�ʷֲ�ֱ��ͼ���£�

��1����A��ʾ�¼�������ֳ�������������50 kg��������A�ĸ��ʣ�
��2����д�������������������������ж��Ƿ���99%�İ�����Ϊ���������ֳ�����йأ�
�������50 kg | �������50 kg | |
����ֳ�� | ||
����ֳ�� |
��3�������������Ƶ�ʷֲ�ֱ��ͼ������������ֳ���������ӽ��бȽ�.
����
P�� | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() ���ⳤΪ
���ⳤΪ![]() ��������.
��������.

��1����֤��ƽ��![]() ƽ��
ƽ��![]() ��
��
��2���������![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ⳤΪa��������ABCD��A1B1C1D1��E��F��P��Q�ֱ���BC��C1D1��AD1��BD���е㣬��֤��

��1��PQ��ƽ��DCC1D1
��2��EF��ƽ��BB1D1D��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com