
(15分) 如图,已知点P在圆柱OO1的底面⊙O上,AB、A1B1分别为⊙O、⊙O1的直径,且A1A⊥平面PAB.
(1)求证:BP⊥A1P;
 (2)若圆柱OO1的体积V=12π,OA=2,∠AOP=120°,求三棱锥A1-APB的体积.
(2)若圆柱OO1的体积V=12π,OA=2,∠AOP=120°,求三棱锥A1-APB的体积.
(3)在AP上是否存在一点M,使异面直线OM与A1B所成角的余弦值为![]() ?若存在,请指出M的位置,并证明;若不存在,请说明理由.
?若存在,请指出M的位置,并证明;若不存在,请说明理由.
(1)证明:因为AP⊥BP,由AA1⊥平面PAB,得AA1⊥BP ……1分
且AP∩AA1=A ……2分; 所以BP⊥平面PAA1 ……3分
 故BP⊥A1P ……4分
故BP⊥A1P ……4分
(2)由题意V=π·OA2·AA1=4π·AA1=12π,解得AA1=3…5分
由OA=2,∠AOP=120°,得∠BAP=30°,BP=2 ……6分
AP=2,∴S△PAB=×2×2=2 ……8分
∴三棱锥A1-APB的体积V=S△PAB·AA1=×2×3=2 ……10分
(3)答:在AP上存在一点M,当M为AP的中点时,使异面直线OM与A1B所成角的余弦值为![]() . ……11分
. ……11分
证明:∵O、M分别为AB、AP的中点,则OM∥BP,且已证BP⊥A1P
∴∠A1BP就是异面直线OM与A1B所成的角 …….13分
在Rt![]() 中,
中,![]()
∴在AP上存在一点M,当M为AP的中点时,使异面直线OM与A1B所成角的余弦值为![]() . …….15分
. …….15分


科目:高中数学 来源: 题型:
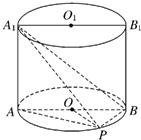 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、圆O1的直径且A1A⊥平面PAB.查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•武昌区模拟)如图,已知点P是圆上C:x2+(y-2
(2011•武昌区模拟)如图,已知点P是圆上C:x2+(y-2| 2 |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
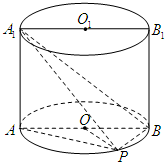 如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,OA=2,∠AOP=120°,三棱锥A1-APB的体积为
如图,已知点P在圆柱OO1的底面圆O上,AB为圆O的直径,OA=2,∠AOP=120°,三棱锥A1-APB的体积为| 8 |
| 3 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•武昌区模拟)如图,已知点P是圆C:x2+(y-2
(2011•武昌区模拟)如图,已知点P是圆C:x2+(y-2| 2 |
| OP |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
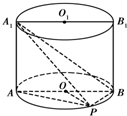 如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.
如图,已知点P在圆柱OO1的底面圆O上,AB、A1B1分别为圆O、O1的直径且A1A⊥平面PAB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com