Question

【题目】如图，有一块矩形空地，要在这块空地上辟一个内接四边形为绿地，使其四个顶点分别落在矩形的四条边上，已知AB=a（a＞2），BC=2，且AE=AH=CF=CG，设AE=x，绿地面积为y．

（1）写出y关于x的函数关系式，并指出这个函数的定义域．
（2）当AE为何值时，绿地面积最大？

Answer 1

【答案】
（1）解：S△AEH=S△CFG= x2，\

S△BEF=S△DGH= （a﹣x）（2﹣x）．\

∴y=SABCD﹣2S△AEH﹣2S△BEF=2a﹣x2﹣（a﹣x）（2﹣x）=﹣2x2+（a+2）x．\

由 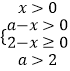，得0＜x≤2\

∴y=﹣2x2+（a+2）x，0＜x≤2

（2）解：当 ，即a＜6时，则x= 时，y取最大值 ．\

当 ≥2，即a≥6时，y=﹣2x2+（a+2）x，在（0，2]上是增函数，

则x=2时，y取最大值2a﹣4\

综上所述：当a＜6时，AE= 时，绿地面积取最大值 ；

当a≥6时，AE=2时，绿地面积取最大值2a﹣4

【解析】（1）先求得四边形ABCD，△AHE的面积，再分割法求得四边形EFGH的面积，即建立y关于x的函数关系式；（2）由（1）知y是关于x的二次函数，用二次函数求最值的方法求解．