
某车间有50名工人,要完成150件产品的生产任务,每件产品由3个A 型零件和1个B 型零件配套组成.每个工人每小时能加工5个A 型零件或者3个B 型零件,现在把这些工人分成两组同时工作(分组后人数不再进行调整),每组加工同一中型号的零件.设加工A 型零件的工人人数为x名(x∈N*)
(1)设完成A 型零件加工所需时间为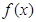 小时,写出
小时,写出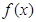 的解析式;
的解析式;
(2)为了在最短时间内完成全部生产任务,x应取何值?
(1) (
(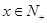
 )(2)32
)(2)32
解析试题分析:(1)生产150件产品,需加工A型零件450个,则完成A型零件加工所需时间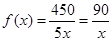 (其中
(其中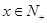 ,且
,且 )……2分
)……2分
(2)生产150件产品,需加工B型零件150个,则完成B型零件加工所需时间 (其中
(其中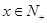 ,且
,且 );……4分zxxk
);……4分zxxk
设完成全部生产任务所需时间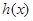 小时,则
小时,则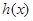 为
为 与
与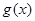 中的较大者,
中的较大者,
令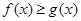 ,则
,则 ,解得
,解得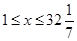
所以,当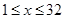 时,
时,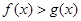 ;当
;当 时,
时,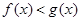
故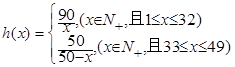 ……7分
……7分
当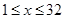 时,
时, ,故
,故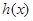 在
在 上单调递减,
上单调递减,
则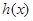 在
在 上的最小值为
上的最小值为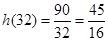 (小时);……9分
(小时);……9分
当 时,
时,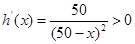 ,故
,故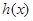 在
在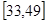 上单调递增,
上单调递增,
则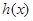 在
在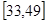 的最小值为
的最小值为 (小时); 11分
(小时); 11分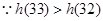 ,
,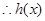 在
在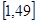 上的最小值为
上的最小值为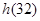 ,
, 为所求,
为所求,
所以,为了在最短时间内完成生产任务,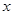 应取32 12分
应取32 12分
考点:函数应用题
点评:本题有一定难度,主要是学生不能很好地理解题意,抓不住关键点:比较两种零件的生产时间的大小,并借此确定函数的最值


科目:高中数学 来源: 题型:解答题
石家庄市为鼓励居民节约用电,采用分段计费的方法计算电费,每月用电不超过100度时,按每度0.52元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
(1)设月用电 度时,应缴电费
度时,应缴电费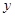 元,写出
元,写出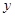 关于
关于 的函数关系式;
的函数关系式;
(2)小明家第一季度缴纳电费情况如下:
| 月份 | 一月 | 二月 | 三月 | 合计 |
| 缴费金额 | 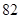 元 元 | 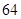 元 元 |  元 元 | 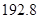 元 元 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知:在函数 的图象上,以
的图象上,以 为切点的切线的倾斜角为
为切点的切线的倾斜角为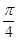 .
.
(Ⅰ)求 ,
,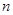 的值;
的值;
(Ⅱ)是否存在最小的正整数 ,使得不等式
,使得不等式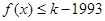 对于
对于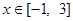 恒成立?如果存在,请求出最小的正整数
恒成立?如果存在,请求出最小的正整数 ;如果不存在,请说明理由;
;如果不存在,请说明理由;
(Ⅲ)求证: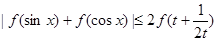 (
( ,
, ).
).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
小明和同桌小聪一起合作探索:如图,一架5米长的梯子AB斜靠在铅直的墙壁AC上,这时梯子的底端B到墙角C的距离为1.4米.如果梯子的顶端A沿墙壁下滑0.8米,那么底端B将向左移动多少米?
(1)小明的思路如下,请你将小明的解答补充完整:
解:设点B将向左移动x米,即BE=x,则:
EC= x+1.4,DC=AC-DC=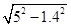 -0.8=4,
-0.8=4,
而DE=5,在Rt△DEC中,由EC2+DC2=DE2,
得方程为: , 解方程得: ,
∴点B将向左移动 米.
(2)解题回顾时,小聪提出了如下两个问题:
①将原题中的“下滑0.8米”改为“下滑1.8米”,那么答案会是1.8米吗?为什么?
②梯子顶端下滑的距离与梯子底端向左移动的距离能相等吗?为什么?
请你解答小聪提出的这两个问题.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地政府鉴于某种日常食品价格增长过快,欲将这种食品价格控制在适当范围内,决定对这种食品生产厂家提供政府补贴,设这种食品的市场价格为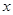 元/千克,政府补贴为
元/千克,政府补贴为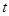 元/千克,根据市场调查,当
元/千克,根据市场调查,当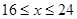 时,这种食品市场日供应量
时,这种食品市场日供应量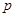 万千克与市场日需量
万千克与市场日需量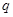 万千克近似地满足关系:
万千克近似地满足关系: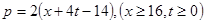 ,
,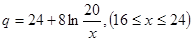 。当
。当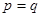 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。
(1)将政府补贴表示为市场平衡价格的函数,并求出函数的值域;
(2)为使市场平衡价格不高于每千克20元,政府补贴至少为每千克多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地西红柿上市时间仅能持续5个月,预测上市初期和后期会因供不应求使价格呈连续上涨势态,而中期又将出现供大于求使价格连续下跌。现有三种价格模拟函数:① ,②
,②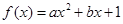 ,③
,③ ,(以上三式中
,(以上三式中 均是不为零的常数,且
均是不为零的常数,且 )
)
(1) 为了准确研究其价格走势,应选择哪种价格模拟函数,为什么?
(2)若 ,求出所选函数
,求出所选函数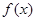 的解析式(注:函数的定义域是
的解析式(注:函数的定义域是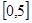 )。其中
)。其中 表示8月1日,
表示8月1日, 表示9月1日,……,以此类推;为保证该地的经济收益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该西红柿将在哪几个月份内价格下跌。
表示9月1日,……,以此类推;为保证该地的经济收益,当地政府计划在价格下跌期间积极拓宽外销,请你预测该西红柿将在哪几个月份内价格下跌。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com