
| A. | $\frac{1}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{1}{6}$ |
分析 先找出二面角的平面角,建立边之间的等量关系,再利用向量法将所求异面直线用基底表示,然后利用向量的所成角公式求出所成角即可.
解答 解:设AB=2,作CO⊥面ABDE,
OH⊥AB,则CH⊥AB,∠CHO为二面角C-AB-D的平面角,
CH=$\sqrt{3}$,OH=CHcos∠CHO=1,
结合等边三角形ABC与正方形ABDE可知此四棱锥为正四棱锥,
则AN=EM=CH=$\sqrt{3}$,$\overrightarrow{AN}$=$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{AB}$),$\overrightarrow{EM}$=$\frac{1}{2}$$\overrightarrow{AC}$-$\overrightarrow{AE}$,
∴$\overrightarrow{AN}•\overrightarrow{EM}$=$\frac{1}{2}$.
故EM,AN所成角的余弦值$\frac{\frac{1}{2}}{\sqrt{3}•\sqrt{3}}$=$\frac{1}{6}$,
故选D.
点评 本小题主要考查异面直线所成的角,考查空间想象能力、运算能力和推理论证能力,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在六面体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,DD1∥平面A1B1BA,DD1∥平面B1BCC1.
如图,在六面体ABCD-A1B1C1D1中,平面ABCD∥平面A1B1C1D1,DD1∥平面A1B1BA,DD1∥平面B1BCC1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=2$\sqrt{3}$,AA1=$\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=2$\sqrt{3}$,AA1=$\sqrt{3}$,AB=2,点D在棱B1C1上,且B1C1=4B1D查看答案和解析>>
科目:高中数学 来源: 题型:选择题
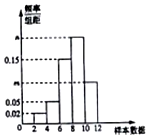 有一个容量为100的样本,其频率分布直方图如图所示,已知样本数据落在区间[10,12)内的频数比样本数据落在区间[8,10)内的频数少12,则实数m的值等于( )
有一个容量为100的样本,其频率分布直方图如图所示,已知样本数据落在区间[10,12)内的频数比样本数据落在区间[8,10)内的频数少12,则实数m的值等于( )| A. | 0.10 | B. | 0.11 | C. | 0.12 | D. | 0.13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com