
【题目】在平面直角坐标系![]() 中
中![]() 设倾斜角为
设倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为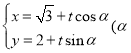 为参数).在以坐标原点
为参数).在以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立的极坐标系中,曲线
轴正半轴为极轴建立的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 与曲线
与曲线![]() 相交于不同的两点
相交于不同的两点![]() .
.
(1)若![]() ,求直线
,求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若![]() 为
为![]() 与
与![]() 的等比中项,其中
的等比中项,其中![]() ,求直线
,求直线![]() 的斜率.
的斜率.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】实验杯足球赛采用七人制淘汰赛规则,某场比赛中一班与二班在常规时间内战平,直接进入点球决胜环节,在点球决胜环节中,双方首先轮流罚点球三轮,罚中更多点球的球队获胜;若双方在三轮罚球中未分胜负,则需要进行一对一的点球决胜,即双方各派处一名队员罚点球,直至分出胜负;在前三轮罚球中,若某一时刻胜负已分,尚未出场的队员无需出场罚球(例如一班在先罚球的情况下,一班前两轮均命中,二班前两轮未能命中,则一班、二班的第三位同学无需出场).由于一班同学平时踢球热情较高,每位队员罚点球的命中率都能达到0.8,而二班队员的点球命中串只有0.5,比赛时通过抽签决定一班在每一轮都先罚球.
(1)定义事件![]() 为“一班第三位同学没能出场罚球”,求事件
为“一班第三位同学没能出场罚球”,求事件![]() 发生的概率;
发生的概率;
(2)若两队在前三轮点球结束后打平,则进入一对一点球决胜,一对一球决胜由没有在之前点球大战中出场过的队员主罚点球,若在一对一点球决胜的某一轮中,某对队员射入点球且另一队员未能射入,则比赛结束;若两名队员均射入或者均射失点球,则进行下一轮比赛. 若直至双方场上每名队员都已经出场罚球,则比赛亦结束,双方通过抽签决定胜负,本场比赛中若已知双方在点球大战,以随机变量![]() 记录双方进行一对一点球决胜的轮数,求
记录双方进行一对一点球决胜的轮数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,倾斜角为
,倾斜角为![]() .以坐标原点
.以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的参数方程和曲线
的参数方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4—4:坐标系与参数方程]
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴,建立极坐标系,直线
轴的非负半轴为极轴,建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设![]() 是曲线
是曲线![]() 上的一个动眯,当
上的一个动眯,当![]() 时,求点
时,求点![]() 到直线
到直线![]() 的距离的最小值;
的距离的最小值;
(2)若曲线![]() 上所有的点都在直线
上所有的点都在直线![]() 的右下方,求实数
的右下方,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国文化中有很多东西喜欢9或9的倍数.如:九连环、九阴白骨爪、降龙十八掌(![]() )、三十六计(
)、三十六计(![]() )、孙悟空七十二变(
)、孙悟空七十二变(![]() )、八十一难(
)、八十一难(![]() )等.若一个三位数的各位数字之和为9,如207,126,则这样的三位数共有________.
)等.若一个三位数的各位数字之和为9,如207,126,则这样的三位数共有________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点![]() 离心率
离心率![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)经过椭圆左焦点![]() 的直线(不经过点
的直线(不经过点![]() 且不与
且不与![]() 轴重合)与椭圆交于
轴重合)与椭圆交于![]() 两点,与直线
两点,与直线![]() :
:![]() 交于点
交于点![]() ,记直线
,记直线![]() 的斜率分别为
的斜率分别为![]() .则是否存在常数
.则是否存在常数![]() ,使得向量
,使得向量![]()
![]() 共线?若存在求出
共线?若存在求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解学生对食堂用餐的满意度,从全校在食堂用餐的3000名学生中,随机抽取100名学生对食堂用餐的满意度进行评分.根据学生对食堂用餐满意度的评分,得到如图所示的率分布直方图,
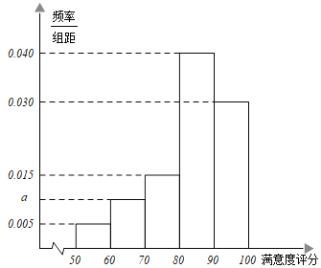
(1)求频率分布直方图中![]() 的值
的值
(2)规定:学生对食堂用餐满意度的评分不低于80分为“满意”,试估计该校在食堂用餐的3000名学生中“满意”的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知2件次品和3件正品混放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所需要的检测费用(单位:元),求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了调查居民对城市共享单车的满意度,随机选取了100人进行问卷调查,并将问卷中的100人根据其满意度评分值按照![]() 分为5组,得到号如图所示的频率分布直方图.
分为5组,得到号如图所示的频率分布直方图.
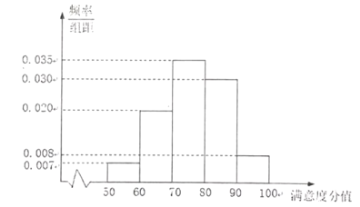
(Ⅰ)求满意度分值不低于70分的人数.
(Ⅱ)已知满意度分值在![]() 内的男性与女性的比为3:4,为提高共享单车的满意度,现从满意度分值在
内的男性与女性的比为3:4,为提高共享单车的满意度,现从满意度分值在![]() 的人中随机抽取2人进行座谈,求这2人中只有一位男性的概率.
的人中随机抽取2人进行座谈,求这2人中只有一位男性的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com