名校课堂系列答案科目：高中数学 来源： 题型：解答题
（12分）某企业拟在2012年度进行一系列促销活动，已知某产品年销量x万件与年促销费用t万元之间满足3-x与t+1成反比例，当年促销费用t=0万元时，年销量是1万件，已知2012年产品的设备折旧、维修等固定费用为3万元，每生产1万件产品需再投入32万元的生产费用。若将每件产品售价定为：其生产成本的150%与“平均每件促销费的一半”之和，则当年生产的商
（1）将2012年的利润y（万元）表示为促销费t（万元）的函数
（2）该企业2012年的促销费投入多少万元时，企业年利润最大？（注：利润=销售收入-生产成
本-促销费，生产成本=固定费用+生产费用）
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
（本题满分10分）已知函数
,(
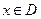)，若同时满足以下条件：
①在D上单调递减或单调递增
② 存在区间[
]
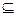D,使在[]上的值域是[]，那么称(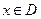)为闭函数。
（1）求闭函数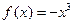
符合条件②的区间[]；
（2）判断函数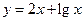
是不是闭函数？若是请找出区间[]；若不是请说明理由；
（3）若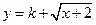
是闭函数，求实数
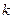的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
15分）经市场调查，某超市的一种小商品在过去的近20天内的销售量（件）与价格（元）均为时间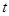
（天）的函数，且销售量近似满足函数
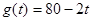（件），价格近似满足函数
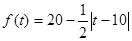（元）。
（1）试写出该种商品的日销售额
函数表达式；
（2）求该种商品的日销售额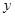
的最大值与最小值。
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
医学上为了研究传染病在传播的过程中病毒细胞的生长规律及其预防措施，将
个病毒细胞注入到一只小白鼠的体内进行试验．在试验过程中，得到病毒细胞的数量与时间的关系记录如下表：
| 时间（小时） | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 病毒细胞总数（个） | | 2 | 4 | 8 | 16 | 32 | 64 |
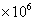个时，小白鼠将死亡，但有一种药物对杀死此种病毒有一定效果，用药后，即可杀死其体内的大部分病毒细胞．
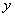与时间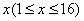
的函数关系式；
）查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
函数
是增函数，
函数
在R上有极值，求使命题“p且q”为真的实数m的取值范围。
的取值范围为（
，
）
（
、
），若
，且对任意实数
（
）不等式
0恒成立．
、
的值；
[－2，2]时，
是单调函数，求实数
的取值范围．
的图像，并指出它的单调区间.
．
的图像；
的解集．
的定义域为
，且满足对于任意
，有
．
的值；
≤
，且
上是增函数，求
的取值范围．